MATE 664 Lecture 05
Diffusion (II)
2026-01-19
Recap of Lecture 04
Key ideas from last lecture:
- Driving forces for diffusion
- Fick’s 1st and 2nd laws of diffusion
- Time-dependent behavior of Fick’s 2nd equation
- Temperature-dependency of diffusivity and activation mechanism
- Introduction to diffusivity measurements
Learning Outcomes
After today’s lecture, you will be able to:
- Recall different types of diffusivities in solids
- Describe basic mechanism in interdiffusion systems
- Analysis the driving force for various diffusion mechanisms
- Analysis of change of reference system in diffusion experiments.
Recap: Fick’s Laws of Diffusion
- 1st law: steady-state diffusion
\[
\vec{J}_i = -D_i \nabla c_i
\]
- 2nd law: time-dependent diffusion
\[
\frac{\partial c}{\partial t} = D_i \nabla^2 c_i
\]
Recap: Different definitions of diffusivities
![]()
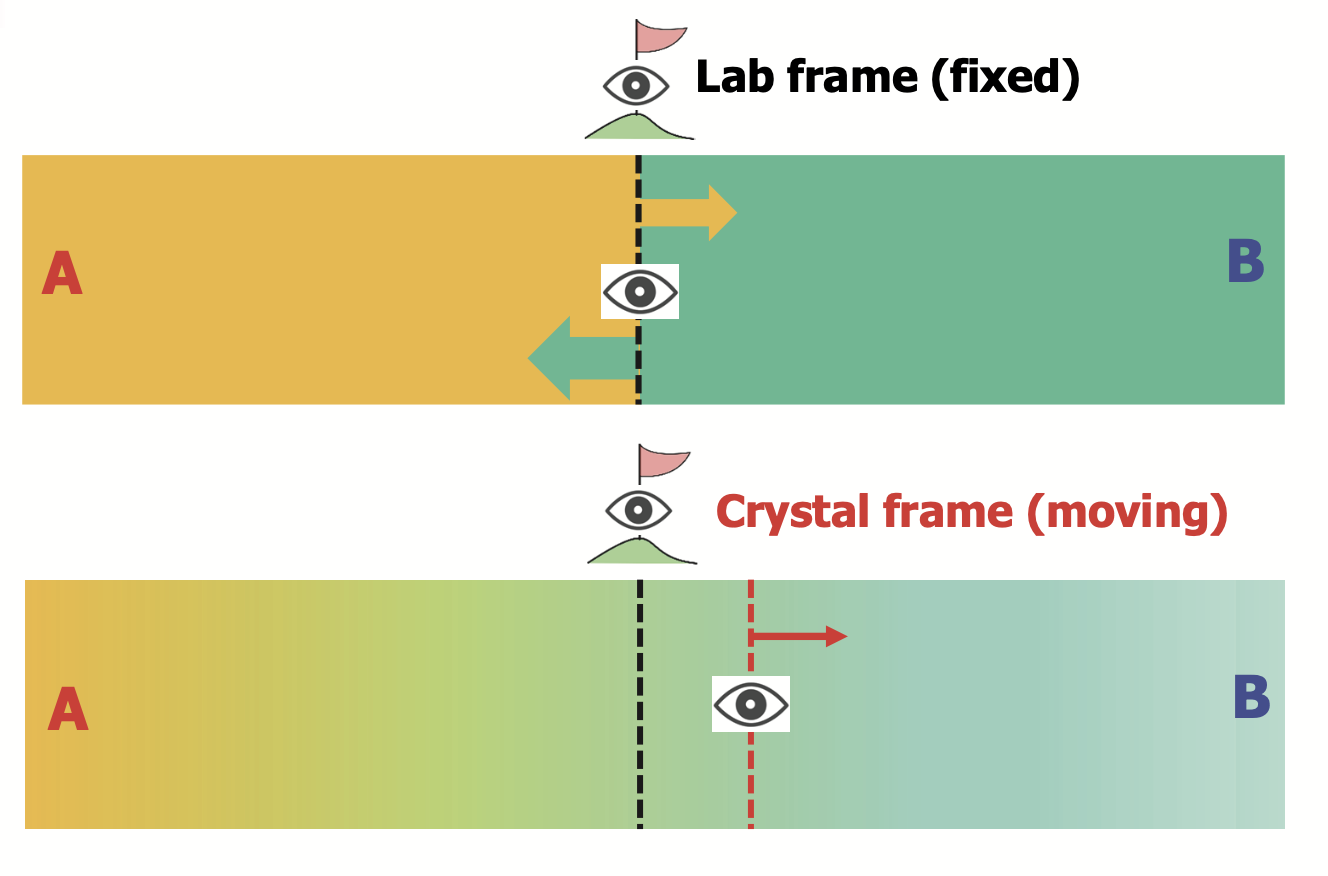
Lattice (C) vs Lab (V) frame
- Self-diffusivity \(D^*\)
- Intrinsic diffusivity \(D_i\) (lattice frame / C-frame; \(\mathtt{C}\) 👉crystal)
- Inter-diffusivity \(\tilde{D}\) (laboratory frame / V-frame; \(\mathtt{V}\) 👉volume-fixed)
We will see a few examples today for more clarification.
Self-Diffusion: Chemically Homogeneous Material
Isotope tracer experiments
Lattice constraint: \[
c_i + c_i^* + c_v = \text{const}
\]
- General “network-constrained” problem
Vacancy concentration often at equilibrium
- Vacancy balance with the source (surface / grain boundary / dislocation)
Flux Relations in Network-Constrained Systems
- Flux driven by chemical potential differences (1D)
Non-radioactive species: \[
J_i = -L_{ii}\frac{\partial (\mu_i - \mu_v)}{\partial x} -L_{i{i}^*}\frac{\partial (\mu_{i^*} - \mu_v)}{\partial x}
\]
Radioactive species: \[
J_{i^*} = -L_{{i^*}{i}}\frac{\partial (\mu_{i} - \mu_v)}{\partial x}
-L_{{i^*}{i^*}}\frac{\partial (\mu_{i^*} - \mu_v)}{\partial x}
\]
Vacancy (zero-flux, why?): \[
J_v = 0
\]
Vacancy Equilibrium Assumption
- \(\mu_v = \text{const}\)
- \(J_v = 0\)
- total flux balance: \[
J_i + J_i^* + J_v = 0
\]
Resulting Self-Diffusion Flux
- Chemical potential gradient: \[
\frac{\partial \mu_{i^*}}{\partial x}
= k_B T \frac{1}{c_i}\frac{\partial c_i}{\partial x}
\]
- Self-diffusion coefficient: \[
D^{*} = k_B T\left(\frac{L_{ii}}{c_i} - \frac{L_{ii^*}}{c_{i^*}}\right)
\]
Self-diffusion summary
- No macroscopic concentration gradient!
- Chemical potential varies locally for \(i\) and \(i^*\)
- Follows the Fick equation!
Self-diffusion in a homogeneous binary solution
- Binary alloy / solution between 1 and 2
- Isotope tracer for 1
- Chemically homogeneous, no lattice change during diffusion
Self-diffusion in binary solution: diffusivity
- We have self-diffusion for 4 species (1, 1\(^*\), 2 and V)
- General flux balance still holds
- Vacancy concentration is uniform
- Still follows Fick’s law.
\[\begin{align}
J_{1^*} &= -k_B T \left[ \frac{L_{11}}{c_1} - \frac{L_{11^*}}{c_{1^*}} \right] \frac{\partial c_{1^*}}{\partial x} \\
&= - D_1^* \frac{\partial c_{1^*}}{\partial x}
\end{align}\]
Diffusion in Inhomogeneous Materials
- Real materials are rarely homogeneous
- Concentration gradients exist by construction
- Diffusion fluxes differ locally in space
- Leads to imbalance of material transport
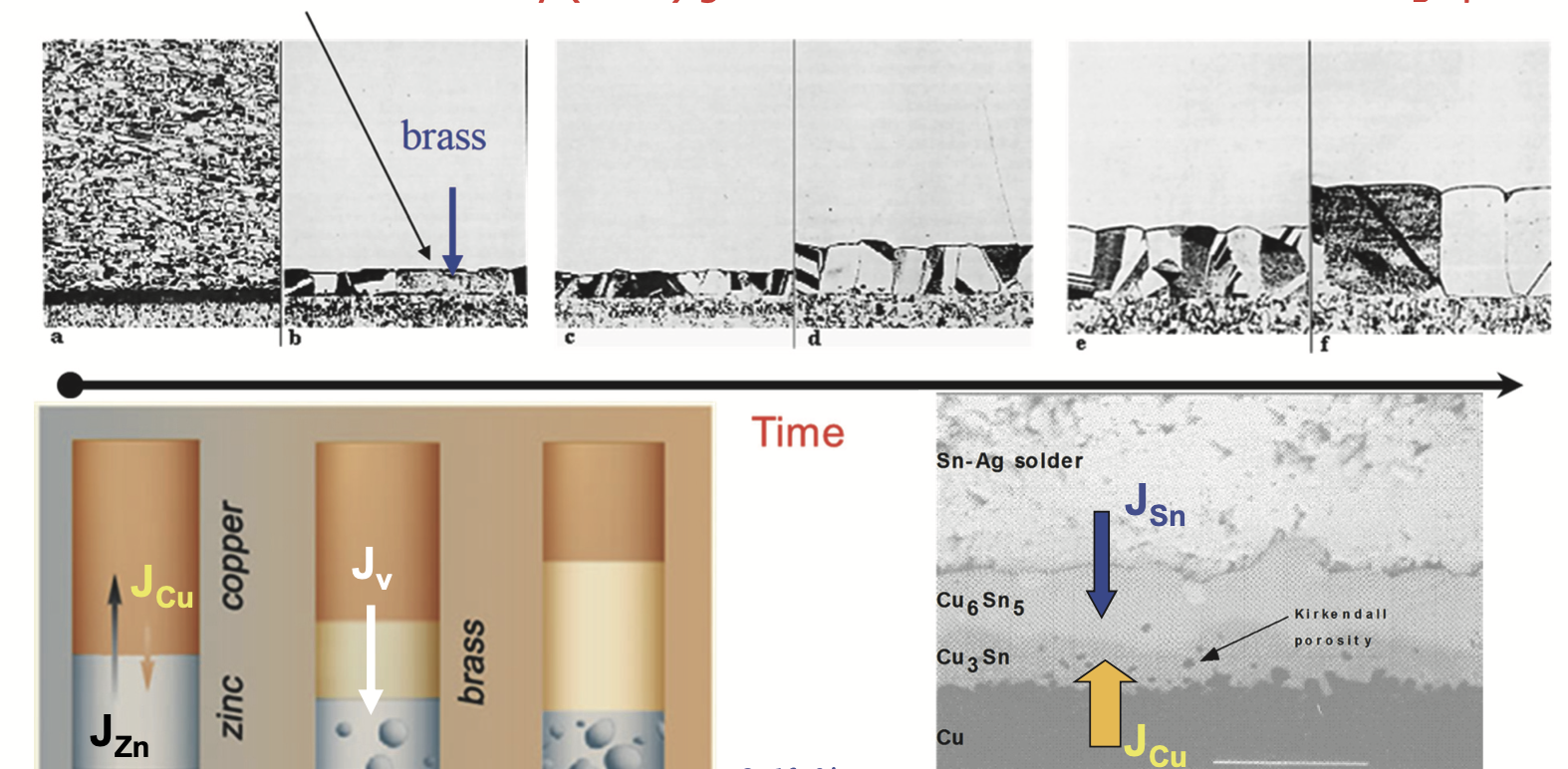
Historical Observation: Boyle (17th Century)
- Robert Boyle observed solid-state diffusion
- Zn penetration into Cu coin → brass formation
- Clear macroscopic evidence of diffusion in solids
- Mechanism not understood until 20th century
Imbalance of Diffusion Fluxes
- Consider a binary diffusion couple A–B
- If \(D_A \neq D_B\)
- Then intrinsic fluxes differ: \[
J_A^{C} \neq - J_B^{C}
\]
- Mass transport is locally unbalanced
Vacancy Mechanism and Imbalance
- Substitutional diffusion proceeds via vacancies
- Site conservation: \[
J_A^{C} + J_B^{C} + J_v^{C} = 0
\]
- Unequal atomic fluxes force a vacancy flux
- Vacancy flux is opposite to faster species
Vacancy Accumulation Issue
- Vacancy flux implies transport of empty sites
- But vacancy concentration remains near equilibrium
- Fast sources/sinks (dislocations, GBs, surfaces)
- Therefore: no long-term vacancy buildup
Kirkendall Effect
- Unequal intrinsic diffusivities
- Net vacancy flux in crystal frame
- Lattice planes shift to accommodate vacancy flow
- Inert markers move relative to sample ends
![]()
C-frame View: Inhomogeneous Materials
- Crystal (C) frame attached to lattice sites
- Atomic fluxes are Fick-like: \[
J_i^{C} = -D_i \frac{\partial C_i}{\partial x}
\]
- Vacancy flux is kinematically constrained
- Lattice assumed locally intact
Intrinsic Diffusivity
- Defined in the crystal frame
- Measures diffusion relative to lattice sites
- Denoted \(D_i\)
- Depends on:
- jump frequency
- vacancy availability
- thermodynamic factor
\[\begin{align*}
J_1^C &= -k_BT [\frac{L_{11}}{c_1} - \frac{L_{12}}{c_2}]\Phi \frac{\partial c}{\partial x} \\
&= -D_1 \frac{\partial c}{\partial x}
\end{align*}\]
Relation to Self-Diffusivity
- Self-diffusion: tracer in homogeneous system
- No net chemical potential gradient
- Intrinsic diffusivity reduces to self-diffusivity: \[
D_i = D_i^{*} \, \Phi
\]
- \(\Phi\): thermodynamic factor
Thought Experiment: Vacancy Diffusion (C-frame)
- Assume \(C_v \approx C_{v,\mathrm{eq}}\)
- Yet \(J_v^{C} \neq 0\)
- Continuity cannot be satisfied by accumulation
- Requires an additional velocity
Origin of Lattice Velocity
Transform flux to lab frame: \[
J_v^{\text{lab}} = J_v^{C} + C_v v
\]
Impose no net vacancy transport in lab frame: \[
J_v^{\text{lab}} = 0
\]
Lattice velocity: \[
v = -\frac{J_v^{C}}{C_v}
\]
Vacancy (V) Frame Basics
- V-frame moves with vacancy flux
- By definition: \[
J_v^{V} = 0
\]
- Atomic fluxes include convective term: \[
J_i^{V} = J_i^{C} + C_i v
\]
Governing Equation in V-frame
- Impose volume conservation: \[
J_1^{V}\Omega_1 + J_2^{V}\Omega_2 = 0
\]
- Leads to single interdiffusion coefficient
- Darken equation emerges naturally
Interdiffusivity
- Defined in volume-fixed (V) frame
- Flux form: \[
J_i^{V} = -\tilde{D} \frac{\partial C_i}{\partial x}
\]
- Interdiffusivity: \[
\tilde{D} = D_1 X_2 + D_2 X_1
\]
Special Case: Interstitial Diffusion
- Interstitial atoms do not occupy lattice sites
- No site conservation constraint
- No lattice drift required
- Interdiffusivity reduces to: \[
\tilde{D} \approx D_{\text{interstitial}}
\]
Summary: Types of Diffusivities
| \(D_i^{*}\) |
lattice |
tracer / self-diffusion |
| \(D_i\) |
C-frame |
intrinsic diffusivity |
| \(\tilde{D}\) |
V-frame |
interdiffusivity |
Summary
- Inhomogeneity leads to flux imbalance
- Vacancy mechanism enforces site conservation
- Lattice velocity resolves vacancy continuity
- Choice of reference frame is essential
- Kirkendall effect is a frame-dependent phenomenon
