MATE 664 Lecture 06

Solution to Diffusion Equations (I)

Dr. Tian Tian

2026-01-21

Recap of Lecture 05

Key ideas from last lecture:

  • Different forms of diffusivities
  • Deriving diffusivity from driving force terms
  • Differentiate reference frames used for diffusion equations

Recap: Intrinsic Diffusivity Expression

For component \(i\) (notation from notes)

\[ D_i^* = k_B T \left(\frac{L_{ii}}{c_i} - \frac{L_{ij}}{c_j}\right) \]

\[ D_i = k_B T\left(\frac{L_{ii}}{c_i}-\frac{L_{ij}}{c_j}\right) \left(1+\frac{\partial \ln \gamma_i}{\partial \ln c_i}\right) \]

whereas

\[ \Phi(c) = 1+\frac{\partial \ln \gamma_i}{\partial \ln c_i} \]

Recap: Interdiffusivity (Binary)

Binary mixture

\[ \tilde D_{12} = D_1 c_2 \Omega_2 + D_2 c_1 \Omega_1 \]

  • \(\Omega_i\): partial molar volume factor in your notation
  • Both C-frame and V-frame still lead to Fick-type equations

Learning Outcomes

After today’s lecture, you will be able to:

  • Interpret Kirkendall effect using lattice (C-frame) vs lab (V-frame)
  • Solve steady-state diffusion (Laplace equation) in common geometries
  • Use non-steady solutions: Gaussian / error function / superposition
  • Use separation of variables and Laplace transform as solution strategies

Remaining Question 1: Kirkendall Effect

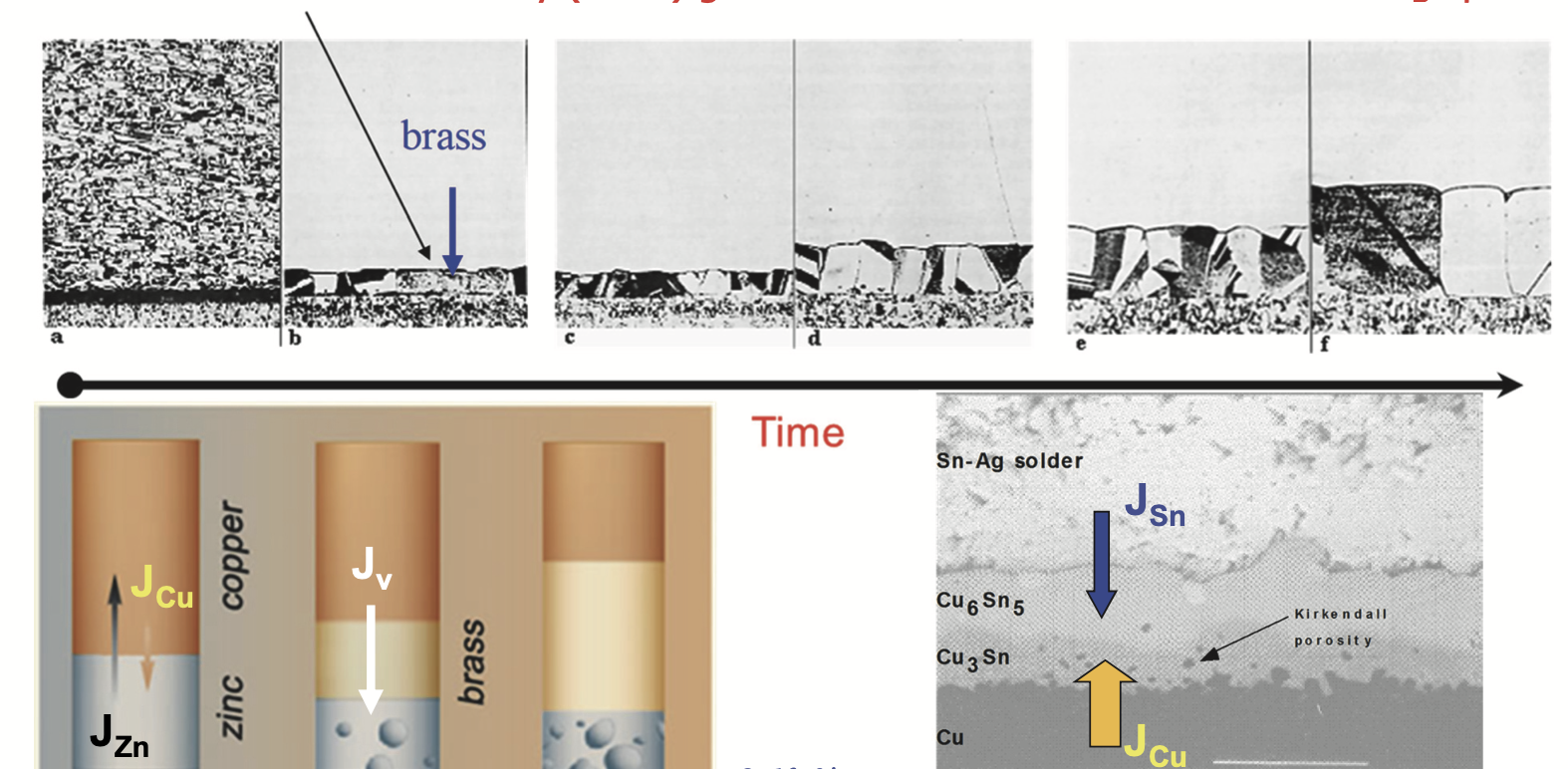
Kirkendall effect demo

Key observation

  • In diffusion couple, markers move relative to lab frame
  • Indicates unequal intrinsic fluxes in lattice frame

C-frame vs V-frame Fluxes

C-frame (lattice frame)

  • net lattice flux can be nonzero: \(J_V^*\neq 0\)

V-frame (lab frame)

\[ J_A^V = -J_B^V,\qquad J_V^V = 0 \]

Interpretation

  • \(J_V^*\neq 0\) but \(J_V^V=0\) implies defect accumulation / depletion

Kirkendall Effect: Physical Meaning

Experimentally measured lattice shift

  • Markers track lattice (or marker plane)
  • Unequal intrinsic fluxes \(\Rightarrow\) vacancy flux
  • Vacancy imbalance \(\Rightarrow\) defect accumulation in control volume
  • Can produce porosity (Kirkendall voids)

Kirkendall Effect: Analog

  • A diffuse faster than B across the membrane
  • \(p_i = c_i RT\)
  • Fixed membrane 👉 expanding voids

Kirkendall Effect: Simulations

See simulation of vacancy mechanism

Credit: Dissemination of IT for the Promotion of Materials Science (DoITPoMS), University of Cambridge

Remaining Question 2: Interstitial Diffusion Setup

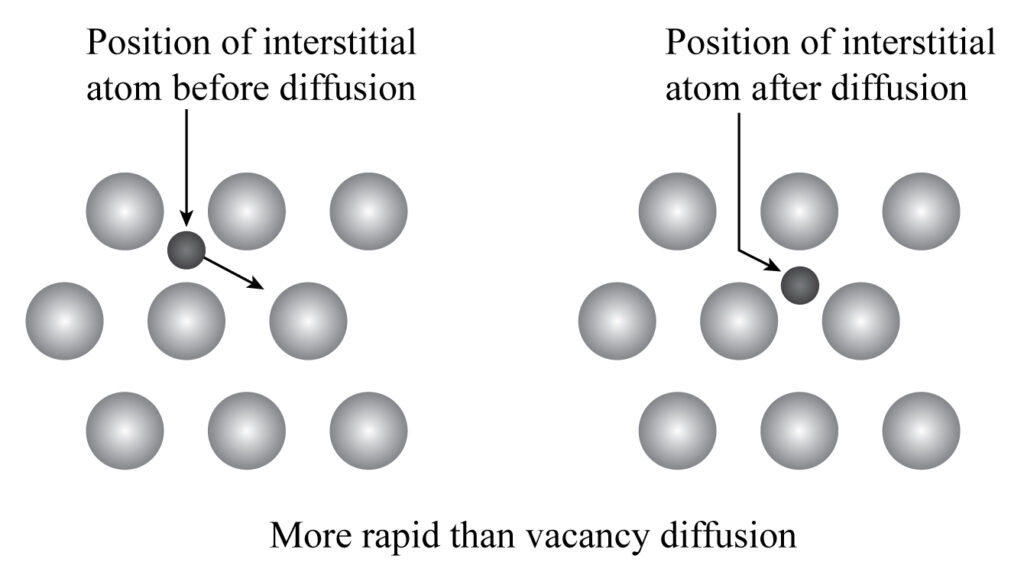
Interstitial diffusion

Model ideas:

  • species 1 diffuses through sites of 2 (interstitial)
  • atoms of 2 are much heavier than 1
  • what is the interdiffusivity \(\tilde{D}\)?

Mobility and Diffusivity in C-frame

C-frame velocity

\[ v_s^* = \frac{M_1}{c_1}\nabla \mu_1 \]

Then

\[ D_1 = M_1 k_B T \]

and (using Onsager coefficient notation)

\[ D_1 = \frac{L_{11}}{c_1} k_B T \]

Connection

  • this matches Nernst–Einstein type relation

V-frame Analysis

Special Case: Diffusivity of 2 → 1 with \(D_2=0\)

  • species 2 immobile: $D_2=0
  • drift velocity related to \(\partial c_1/\partial x\)
  • similar to “diffusion through solvent” in mass transfer
\[\begin{align} J_1^V &= -D_1 \frac{\partial c_1}{\partial x} + c_1 (D_1 - 0) \Omega_1 \frac{\partial c_1} {\partial x} \\ &= -D_1 \left( 1 - c_1 \Omega_1 \right) \frac{\partial c_1} {\partial x} \\ \end{align}\]

V-frame: Effective Diffusivity

The interdiffusivity now becomes:

\[\begin{align} \tilde{D} &= D_1 \Omega_2 c_2 \\ &= D_1 x_2 \end{align}\]
  • \(x_2\) is the fraction of lattice particles (usually 1).
  • interdiffusivity depends on “how many sites” the smaller species can use
  • this expression only applicable for interstitial diffusion!

Driving Forces Beyond Chemical Potential

We often used \(\mu_i\) as driving force for diffusion, but other contributions exist.

Generalized “diffusion potential”:

\[ \Phi_i = \mu_i + \sum_j \eta_j \]

  • vacancy mechanism / site availability
  • electromigration
  • external pressure / stress effects
  • capillarity / surface curvature effects
  • etc.

How Do We Determine \(D\)?

General experimental workflow:

  • impose initial concentration + geometry
  • evolve for time \(t>0\)
  • measure profile \(c(x,t)\) (or length scale)
  • fit to model solution \(\Rightarrow D\)

Forward Problem vs Inverse Problem

Given

  • geometry + initial/boundary conditions
  • candidate \(D\)

Predict

  • concentration profile \(c(x,t)\)

Inverse

  • infer \(D\) from measured \(c(x,t)\)

What Do We Learn In The Following Lectures?

  • We want analytical + numerical solutions to the diffusion equations (Fick’s laws)

  • Start with steady state, then non-steady state.

  • Covering general formula, and geometries

Fick’s Second Law (1D, constant \(D\))

Assuming homogeneous isotropic constant \(D\)

\[ \frac{\partial c}{\partial t}=D\frac{\partial^2 c}{\partial x^2} \]

To solve we must specify

  • initial condition: \(c(x,0)\)
  • boundary conditions: \(c(0,t)\), \(c(L,t)\) or flux BC

Part I: Steady State Diffusion

Steady state

\[ \frac{\partial c}{\partial t}=0 \quad\Rightarrow\quad \nabla^2 c = 0 \]

This is Laplace equation, having solution in 1D:

\[ \frac{d^2 c}{dx^2}=0 \Rightarrow c(x)=C_1 x + C_2 \]

1D Steady State: Dirichlet BC Example

If \(c(0)=c^0\) and \(c(L)=c^L\)

Then

\[ c(x)=c^0+\frac{c^L-c^0}{L}x \]

and flux

\[ J=-D\frac{dc}{dx} = -D\frac{c^L-c^0}{L} \]

Cylindrical Steady State (Radial)

For axisymmetric \(c=c(r)\)

\[ \nabla^2 c=\frac{1}{r}\frac{d}{dr}\left(r\frac{dc}{dr}\right)=0 \]

Integrate twice

\[ c(r)=k_1\ln r+k_2 \]

Cylinder: Apply BC at \(r_1, r_2\)

If \(c(r_1)=c_1\) and \(c(r_2)=c_2\)

Then

\[ c(r)=c_1+\frac{c_2-c_1}{\ln(r_2/r_1)}\ln\left(\frac{r}{r_1}\right) \]

Spherical Steady State (Radial)

For \(c=c(r)\)

\[ \nabla^2 c=\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dc}{dr}\right)=0 \]

Integrate to get

\[ c(r)=-\frac{k_1}{r}+k_2 \]

Sphere: Apply BC at \(r_1, r_2\)

If \(c(r_1)=c_1\), \(c(r_2)=c_2\)

One convenient form

\[ c(r)=c_1+\frac{c_2-c_1}{\left(\frac{1}{r_2}-\frac{1}{r_1}\right)} \left(\frac{1}{r}-\frac{1}{r_1}\right) \]

Spatially Varying Diffusivity in Steady State

Notes: still solvable if \(D\) depends on 1 variable (e.g. \(x\) or \(r\))

Steady 1D with constant flux \(J\)

\[ J=-D(x)\frac{dc}{dx}=\text{const} \]

So

\[ \frac{dc}{dx}=-\frac{J}{D(x)} \Rightarrow c(x)=c(x_0)-J\int_{x_0}^x\frac{1}{D(\xi)}\,d\xi \]

Often requires numerical integration for \(D(\xi)\).

  • Dirchlet boundary 👉 directly integration
  • Neumann boundary 👉 need to fix \(dc/dx\) at boundary

Part II: Non-steady State Diffusion

Different strategies

  • superposition with known “source” solutions
  • separation of variables (finite domains)
  • Laplace transform (initial condition handling)
  • numerical methods (general geometry / \(D(c)\))

Method 1: Superposition of Known Solutions

Use linearity of diffusion equation

If \(c_a\) and \(c_b\) satisfy the PDE and BCs, then

\[ c = c_a + c_b \]

also satisfies (with compatible IC/BC decomposition).

Inifinite Space: Half-Half Situation

Geometry: \(x\ge 0\)

I.C.

  • \(c(x<0,t=0)=c_L\)
  • \(c(x>0,t=0)=c_R\)

Solution form

\[ c(x,t)=\frac{c_L + c_R}{2} + \frac{c_L-c_R}{2}\,\operatorname{erf}\left(\frac{x}{\sqrt{2Dt}}\right) \]

How do we get here?

Limits and Checks

  • \(t\to 0^+\): \(\operatorname{erfc}(x/(2\sqrt{Dt}))\to 0\) for \(x>0\) ⇒ \(c\to c_B\)
  • \(x\to 0\): \(\operatorname{erfc}(0)=1\) ⇒ \(c(0,t)=c_A\)
  • \(x\to\infty\): \(\operatorname{erfc}(\infty)=0\) ⇒ \(c\to c_B\)

Next Steps

  • Apply these solutions to real diffusion experiments
  • Extract \(D\) by fitting measured \(c(x,t)\)
  • Extend to variable \(D(c)\) and coupled diffusion (later)