MATE 664 Lecture 11

Diffusion in Defect and Material Imperfections

Dr. Tian Tian

2026-02-09

Recap of Lecture 10

Key ideas from last lecture:

  • Diffusion equations for solids
  • Link Einstein’s equation to Arrhenius equation
  • Emergence of activation enthalpy / entropy
  • Vacancy formation free energy and diffusion

Learning outcomes

After this lecture, you will be able to:

  • Apply the free energy-dependent diffusion equations to systems with defects and material imperfections
  • Understand how intrinsic and extrinsic defect in ionic materials are formed
  • Analyze intrinsic / extrinsic diffusion regimes in ionic materials
  • Understand material imperfections as the diffusion shortcuts

What does diffusion in real materials look like?

  • Real solids are not perfect crystals
  • Defects control transport properties
  • Ionic diffusion shows rich temperature dependence
  • Same Einstein framework, new physics inside

Base line: vacancy-mediated diffusion in metals

  • Diffusion = random walk of atoms via vacancies
  • Diffusivity related to both vacancy density (controlled by \(G_v^f\)) and vacancy jumping (controlled by \(G_v^m\))
\[\begin{align} D_A &= \frac{z \langle r^2 \rangle \nu}{6} \exp\!\left(\frac{S_v^{f} + S_v^{m}}{k_B}\right) \exp\!\left(-\frac{H_v^{f} + H_v^{m}}{k_B T}\right) \, f \end{align}\]

Defect-mediated diffusion in ionic crystals

  • Defects in ionic crystals are more complex than in metal
  • Charge neutrality has to be conserved
  • More than one single defect species are involed
  • In other words, defects always come in pairs in ionic solids

Schottky and Frenkel defects in ionic crystals

  • Schottky defects: missing both positive and negative species
  • Frenkel defects: one charged species moved to other site

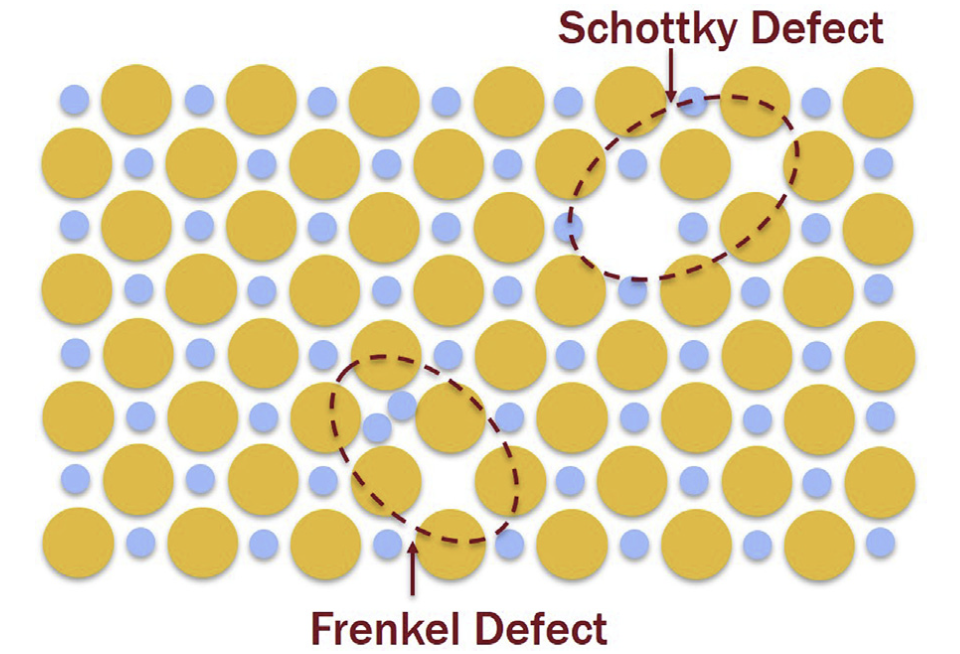
Comparison between Schottky and Frenkel defects

Ionic defects: Kröger-Vink (KV) notation

  • Formula \(X^Z_Y\)
  • X = what is at the site (Element or Vacancy)
  • Y = what site is defective (Element or i)
  • Z = effective charge at the site (• = +; ’= –)

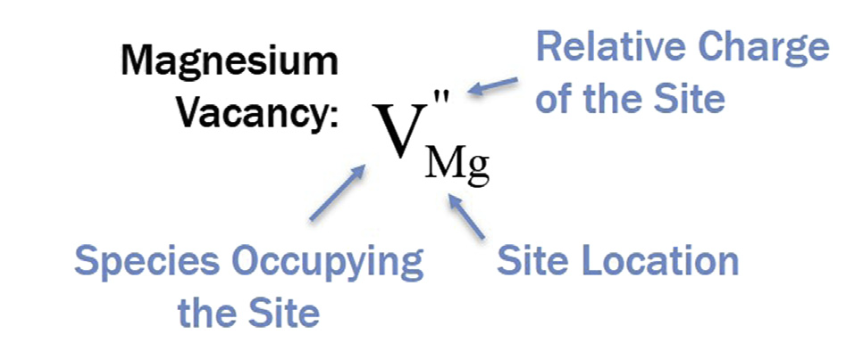
Example of KV notation

KV notation for Schottky defects

Example: Schottky defects in MgO (anion + cation vacancies)

  • Formation reaction

    \[ \text{null} \rightarrow V_{\mathrm{Mg}}^{''} + V_{\mathrm{O}}^{\bullet\bullet} \]

  • Equilibrium condition

    • \(G_S^f\): formation free energy for Schottky defects (per reaction)

    \[ K_S = [V_{\mathrm{Mg}}^{''}][V_{\mathrm{O}}^{\bullet\bullet}] = \exp\!\left(-\dfrac{G_S^{f}}{kT}\right) \]

  • Charge neutrality

    \[ [V_{\mathrm{Mg}}^{''}] = [V_{\mathrm{O}}^{\bullet\bullet}] \]

KV notation for Frenkel defects

Example: Frenkel pairs in LiF (Lithium escaping to interstitial sites)

  • Formation reaction

    \[ \mathrm{Li}_{\mathrm{Li}}^{\times} \rightarrow V_{\mathrm{Li}}^{'} + \mathrm{Li}_i^{\bullet} \]

  • Equilibrium condition

    • \(G_F^f\): formation free energy for Schottky defects (per reaction)

    \[ K_F = [V_{\mathrm{Li}}^{'}][\mathrm{Li}_i^{\bullet}] = \exp\!\left(-\dfrac{G_F^{f}}{kT}\right) \]

  • Charge neutrality
    \([V_{\mathrm{Li}}^{'}] = [\mathrm{Li}_i^{\bullet}]\)

Intrinsic vs extrinsic defects

  • Intrinsic defects are those controlled by thermodynamics \(G_S^f\), \(G_F^f\) or \(G_V^f\)
  • Extrinsic defects are those defects added to the ionic crystal via doping

Example of Extrinsic defects: CdCl\(_2\) in NaCl

  • Dopant incorporation reaction
    \[ \mathrm{CdCl}_2 \rightarrow \mathrm{Cd}_{\mathrm{Na}}^{\bullet} + 2\,\mathrm{Cl}_{\mathrm{Cl}}^{\times} + V_{\mathrm{Na}}^{'} \]

  • Extrinsic defect concentration
    \[ [V_{\mathrm{Na}}^{'}]_{\text{ext}} = [\mathrm{Cd}_{\mathrm{Na}}^{\bullet}] = [\mathrm{CdCl}_2] \]

  • Total vacancy concentration
    \[ [V_{\mathrm{Na}}^{'}] \approx [V_{\mathrm{Na}}^{'}]_s + [V_{\mathrm{Na}}^{'}]_{\text{ext}} = \frac{\exp\!(-\dfrac{G_S^{f}}{k_B T})}{ [\mathrm{CdCl}_2]} + [\mathrm{CdCl}_2] \]

Diffusivity of ionic species

  • We can still use the vacancy exchange mechanism for the diffusivity of ionic species
  • For f.c.c. lattice the neighbor sites of same charge, the multiplicity \(z=6\).
  • E.g. Na\(^+\) exchanges with its own vacancy \(V_{\mathrm{Na}}^{'}\)
  • \([V_{\mathrm{Na}}^{'}]\) depends on the \(T\)-regime!
\[\begin{align} D_{\mathrm{Na}} &= [V_{\mathrm{Na}}^{'}]\, f\,\lambda^2\,\nu\, \exp\!\left(-\frac{G_{\mathrm{Na}}^{m}}{kT}\right) \end{align}\]

Intrinsic vs extrinsic regimes

  • Extrinsic: vacancy dominated by doped materials
    • Low-\(T\) regime (high \(1/T\))
\[\begin{align} D_{\mathrm{Na,ext}} &= [\mathrm{CdCl}_2]\, f\,\lambda^2\,\nu\, \exp\!\left(\frac{S_{\mathrm{Na}}^{m}}{k}\right) \exp\!\left(-\frac{H_{\mathrm{Na}}^{m}}{kT}\right) \end{align}\]
  • Intrinsic: vacancy dominated by thermal dissociation
    • High-\(T\) regime (low \(1/T\))
\[\begin{align} D_{\mathrm{Na,int}} &= f\,\lambda^2\,\nu\, \exp\!\left(\frac{S_{S}^{f}}{2k}\right) \exp\!\left(\frac{S_{\mathrm{Na}}^{m}}{k}\right) \exp\!\left(-\frac{H_{S}^{f}}{2kT}\right) \exp\!\left(-\frac{H_{\mathrm{Na}}^{m}}{kT}\right) \end{align}\]

Two-regimes in the Arrhenius plot

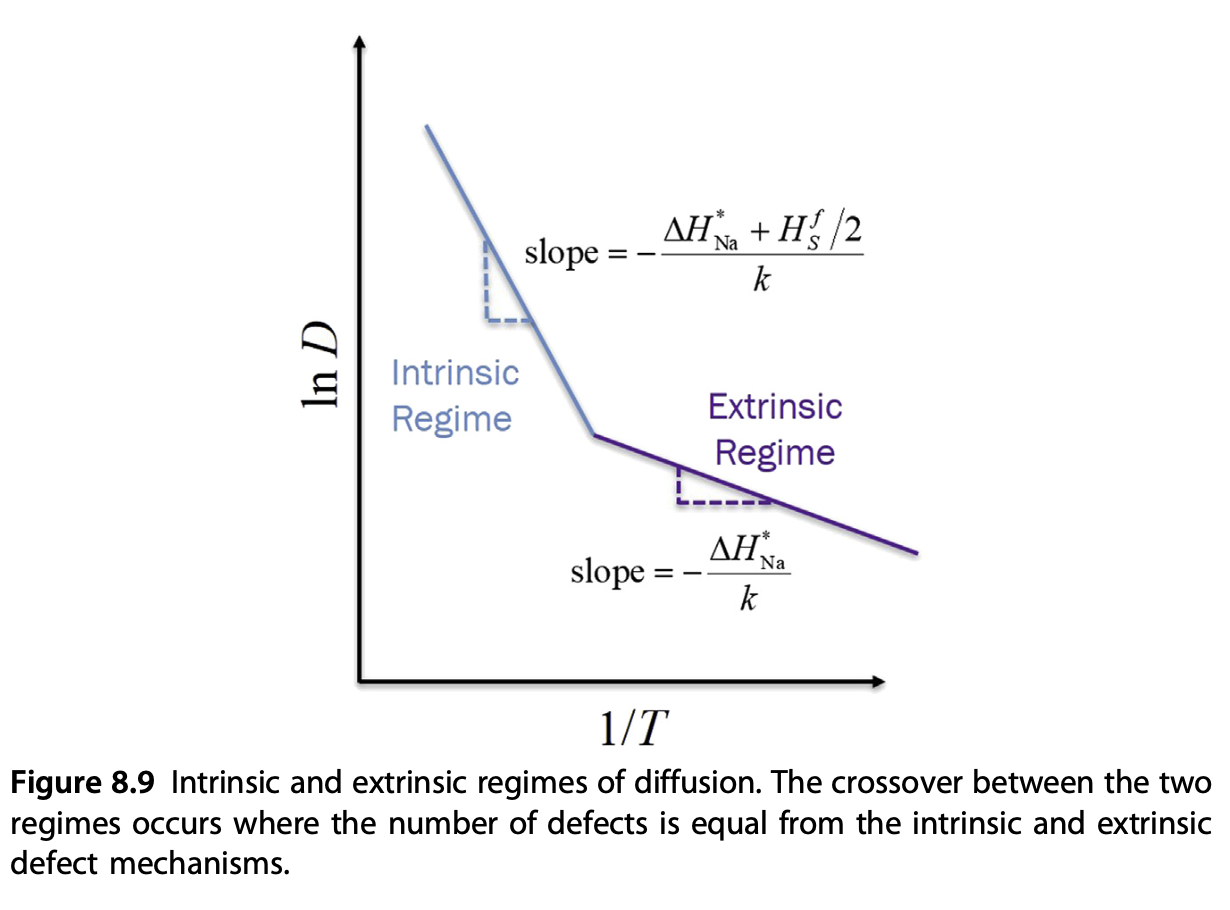
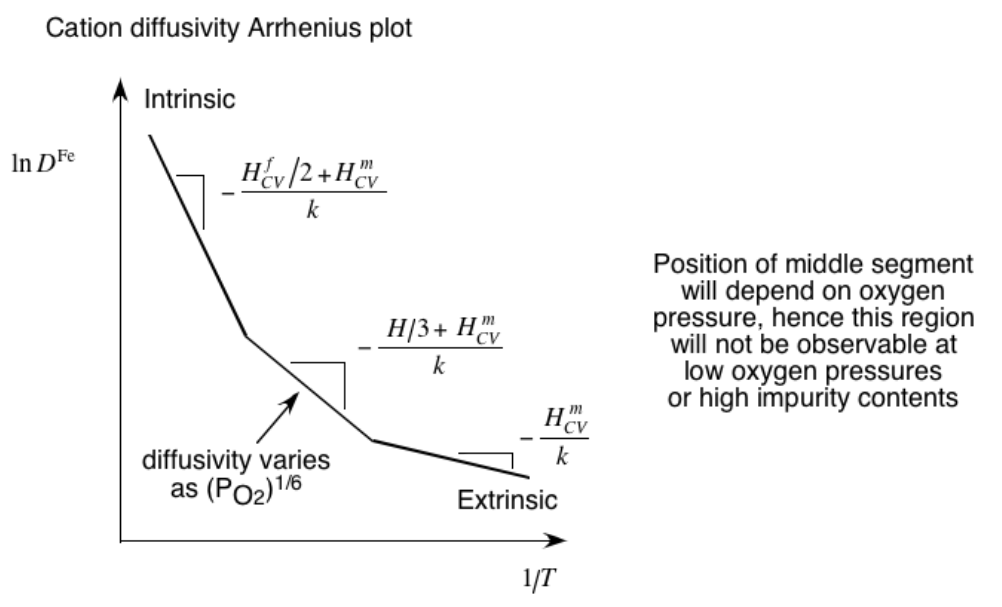
More regimes in Arrhenius plot

  • Example: cation diffusion in FeO during oxidation
  • Equilibrium depends on both \(G^f\) and \(p(O_2)\)
  • Multiple regimes!

Multiple-regime diffusion in polycrystalline materials

Arrhenius plot for diffusion on imperfections

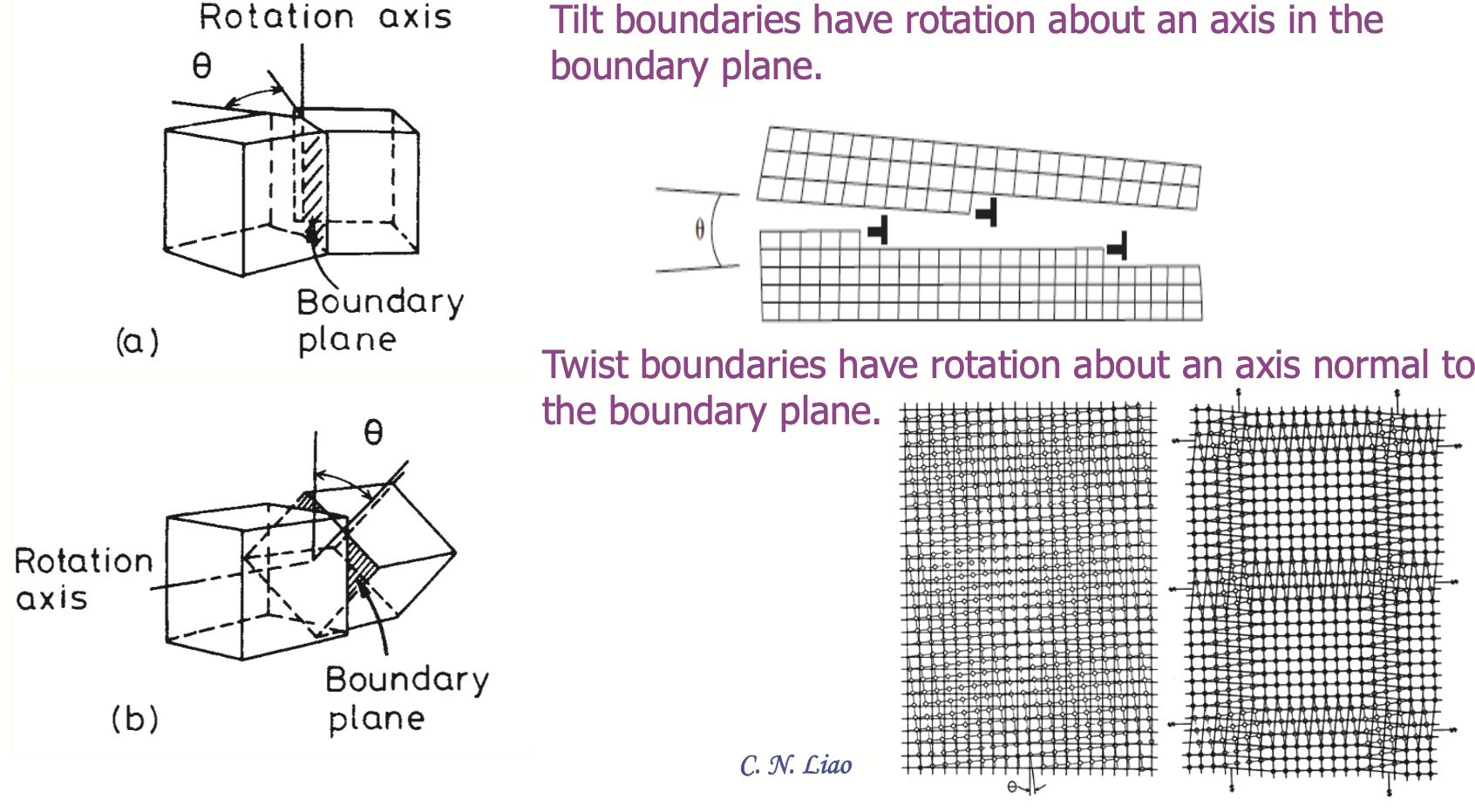
Diffusion paths at crystal imperfections

  • Diffusion can occur along non-bulk pathways
  • Typical crystal imperfections
    • Grain boundary and interface diffusion: 2D
    • Free surface diffusion: 2D
    • Dislocation (pipe) diffusion: 1D
    • Vacancy / defect: 0D
  • Imperfections are associated with lower migration / activation energy!
  • Think as “shortcuts” during diffusion

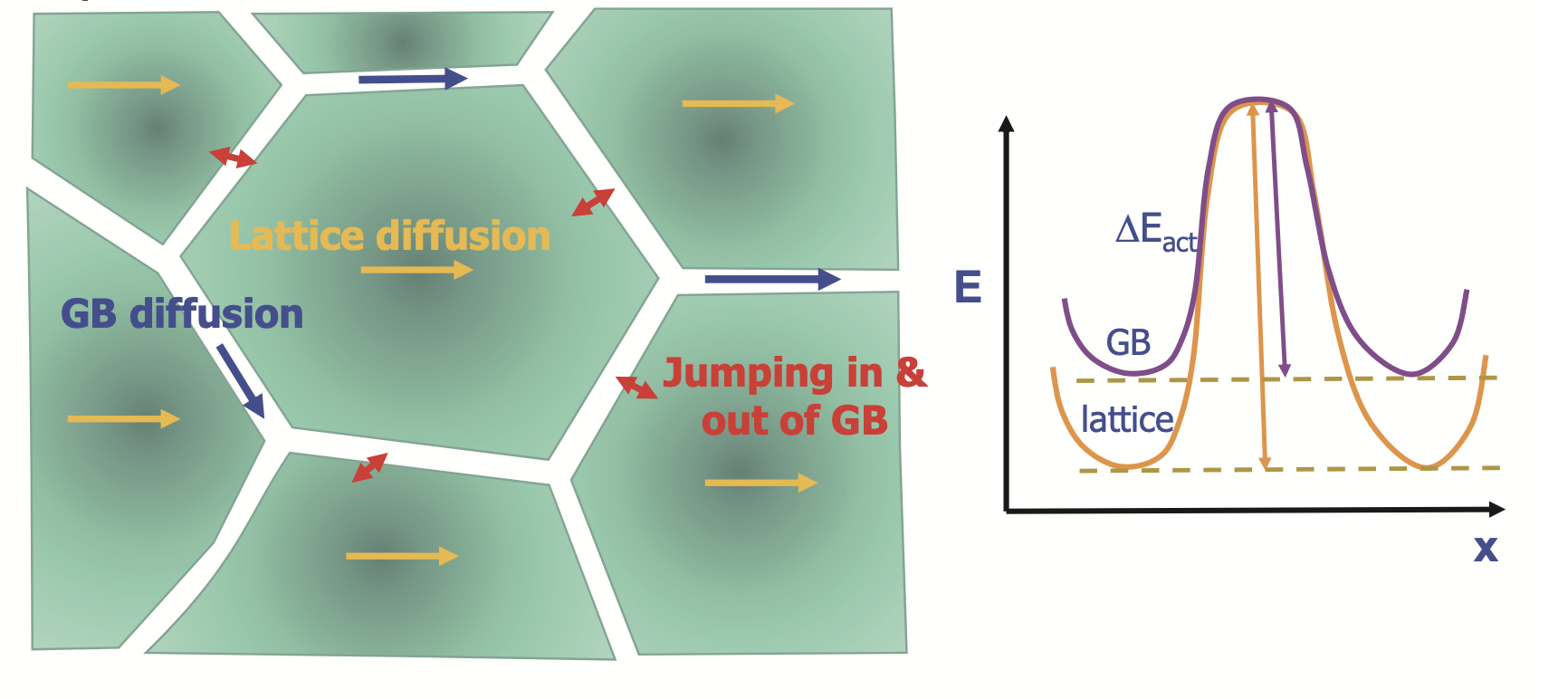
Imperfection 1: grain boundaries

Grain boundary diffusion

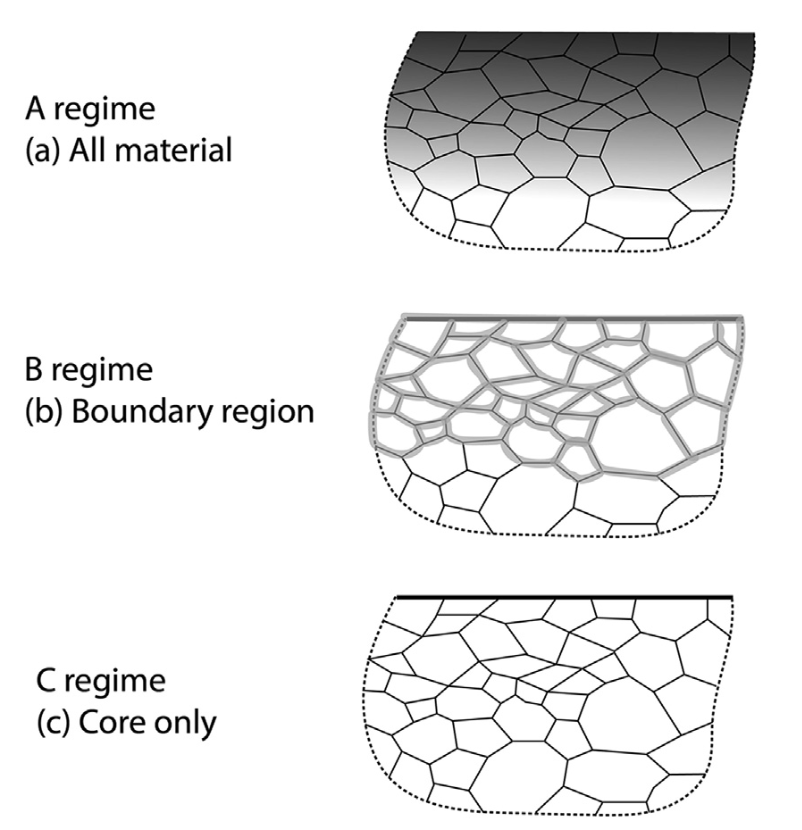
Harrison’s ABC model for GB diffusion

A foreign material is coated on the top of a polycrystalline metal. The degree of penetration can be studied by comparing the timescale \(t\), interatomic distance \(\lambda\) and grain size \(s\)

  • All regime
    • \(D_{XL} t > s^2\)
    • \(D_B t > s^2\)
  • Boundary regime
    • \(D_{XL} t \approx \lambda^2\)
    • \(D_B t > \lambda^2\)
    • coupled short-circuit and bulk diffusion
  • Core regime
    • \(D_{XL} t < \lambda^2\)
    • \(D_B t > \lambda^2\)
    • diffusion confined to imperfections

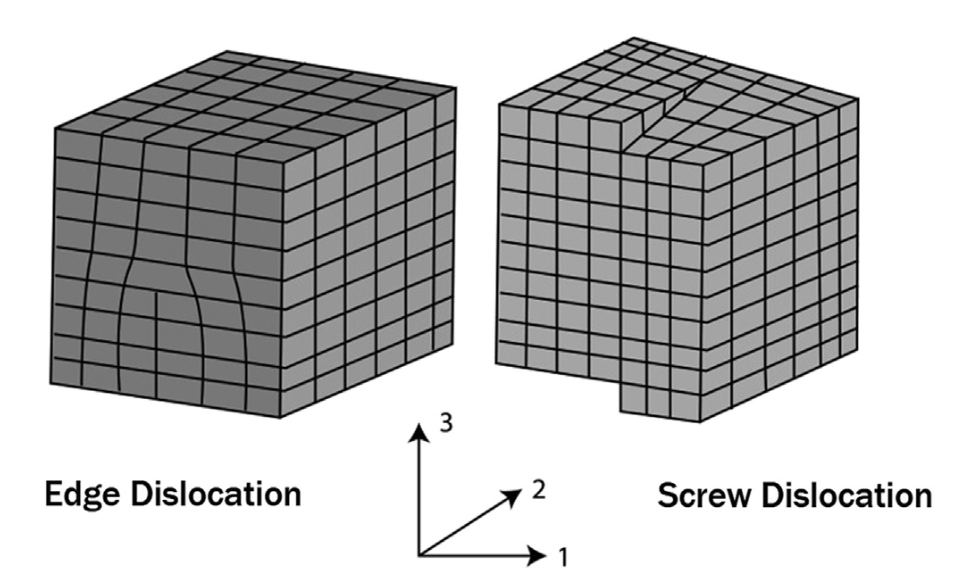
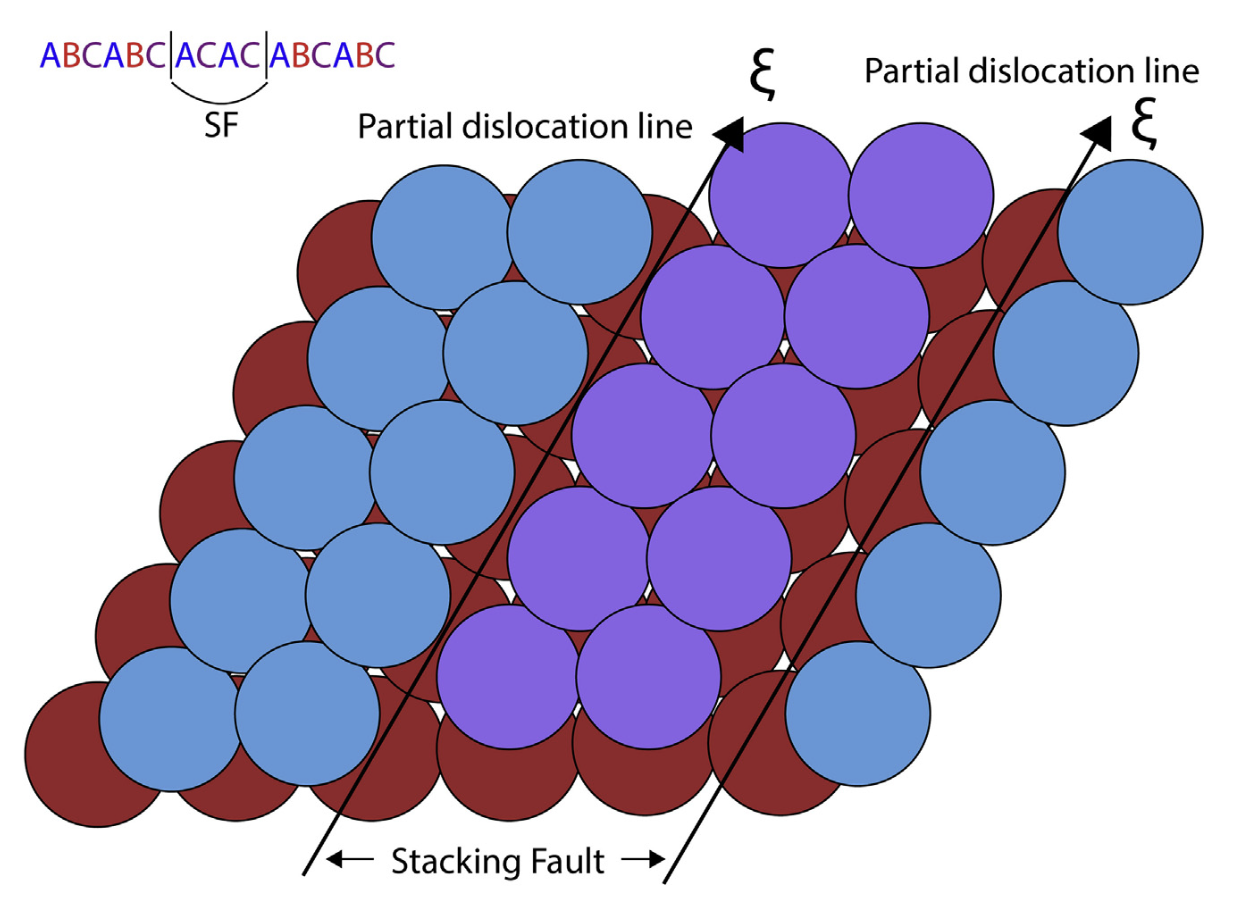
Dislocation imperfections (line defect)

Edge and screw dislocations

Partial dislocations

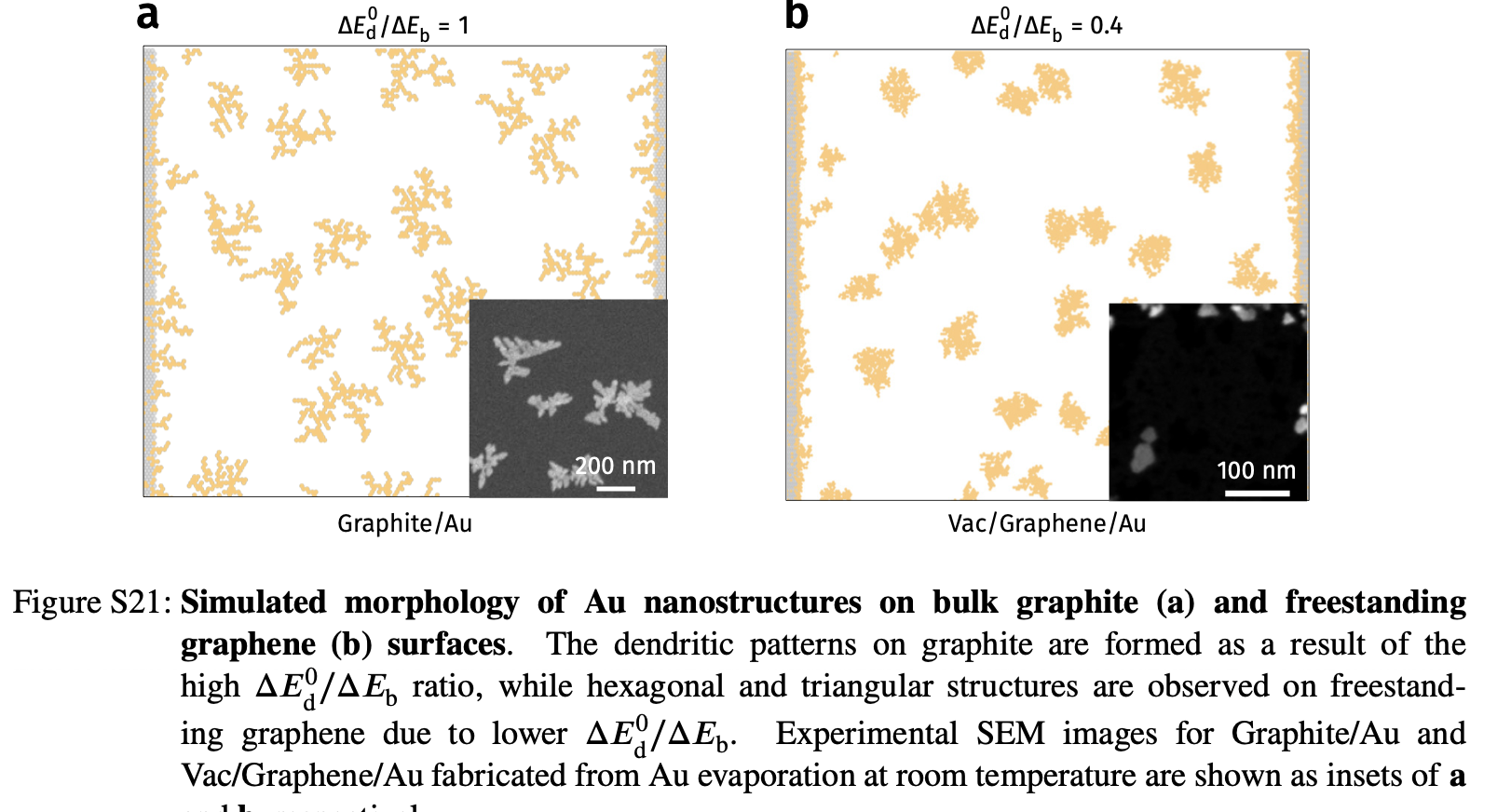
Example of diffusion along imperfection: deposition on graphene

  • See Vagli and Tian et al. Nat Commun 2025, 16, 7726.
  • Diffusivity change on free graphene surface can be probed by deposition geometry!

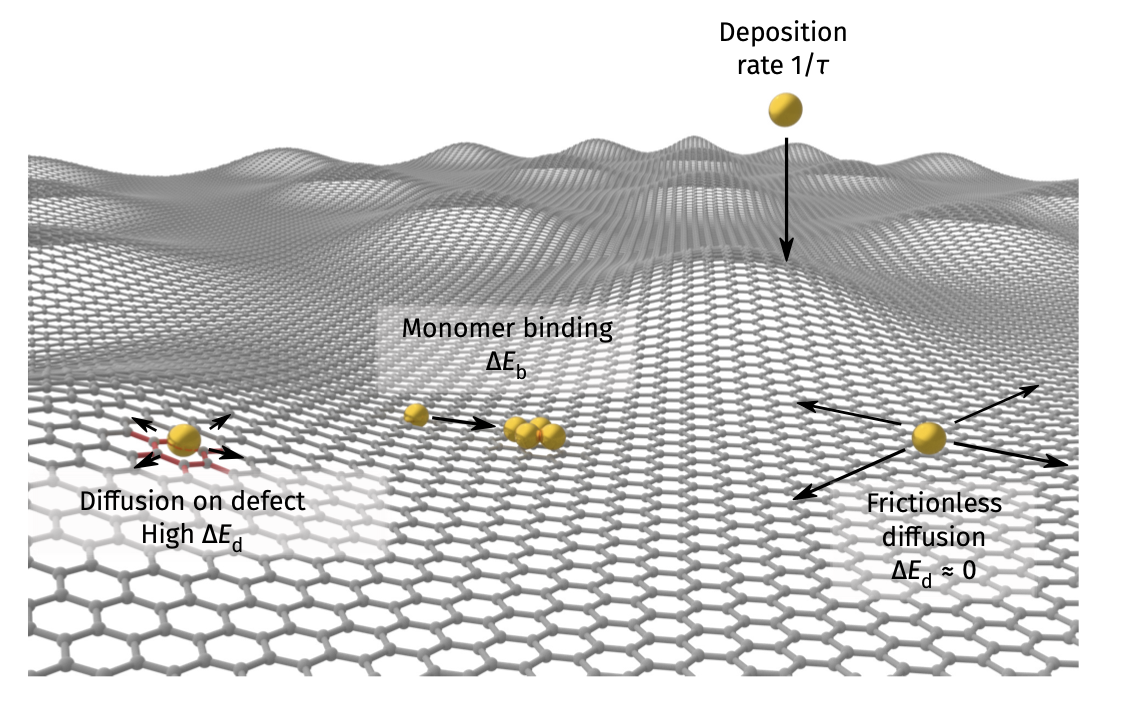
Deposition on Graphene - theoretical simulations

  • Kinetic Monte Carlo (kMC) assuming different diffusion barrier on imperfections
  • Faster diffusion direction –> lower density

Deposition on Graphene - theoretical simulations

  • Kinetic Monte Carlo (kMC) assuming different diffusion barrier on imperfections
  • Faster diffusion direction –> lower density

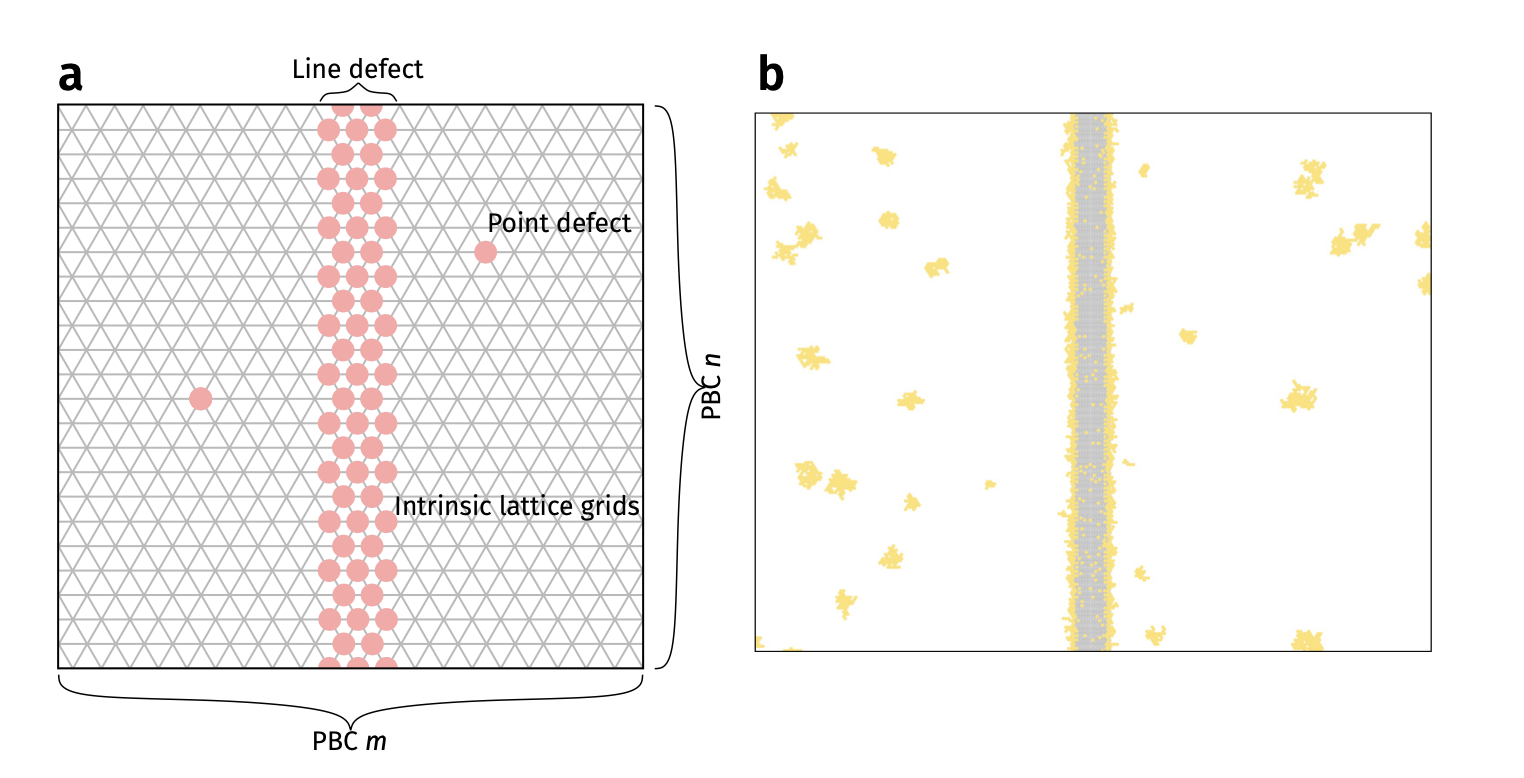
Deposition on Graphene - KMC vs experiments

Summary

In this lecture, we reviewed a few sample cases where diffusion is dominated by crystal defects and imperfections

  • Diffusion by ionic defects – multiple Arrhenius regimes
  • Diffusion by imperfections – shortcut diffusion compared with bulk diffusion
  • Example of interface mediated diffusion – 2D material