CHE 318 Lecture 03

Molecular Diffusion in Gases: General Solutions

Dr. Tian Tian

2026-01-09

Recap

  • Governing equation for diffusion binary mixture gas systems \[ N_{A} = -c_T D_{AB} \dfrac{d x_A}{dz} + x_A(N_A + N_B) \]
  • Case 1: equimolar counter diffusion (EMCD)
    • \(N_A + N_B = 0\)
    • \(N_A = -c_T D_{AB} \dfrac{d x_A}{d z}\)
    • Linear \(x_A\), \(c_A\) and \(p_A\) profiles
    • \(N_A = \dfrac{D_{AB}}{RT(z_2 - z_1)}(p_{A1} - p_{A2})\)
  • Case 2: diffusion through stagnant B
    • \(N_B = 0\)
    • \(N_A(1 - x_A) = -c_T D_{AB}\dfrac{d x_A}{dz}\)
    • Usually in log-mean pressure form
    • \(N_A = \dfrac{D_{AB}}{RT(z_2-z_1)} \dfrac{p_T}{p_{Bm}} \left(p_{A1} - p_{A2}\right)\)

Office Hour

  • Wednesday 11:15 - 12:15
  • DICE 12-245
  • Can take place in other meeting rooms if many people are attending
  • Please use seminar time wisely for assignment questions!

Learning Outcomes

After today’s lecture, you will be able to:

  • Derive general solution for mass transport in binary gas mixture
  • Define the conditions for each cases we have studied so far
  • Formulate governing equations for various case systems
  • Apply general solution to defined problem
  • Analyze pressure / concentration profile

Deriving the General Solution (I)

General case for steady state (S.S) transport

  • \(N_B = k N_A\) (\(k\) is a constant. why?)
  • Only \(x_A\) (or \(c_A\), \(p_A\)) dependent on \(z\), not \(N_A\) or \(N_B\) 👉 separation of variables!
\[\begin{align} N_A - x_A(N_A + N_B) &= -D_{AB}c_T \dfrac{d x_A}{dz}\\ \frac{dz}{D_{AB} c_T} &= -\dfrac{dx_A}{N_A - x_A (N_A + N_B)} \\ \int_{z_1}^{z_2} \frac{dz}{D_{AB} c_T} &= \int_{x_{A1}}^{x_{A2}} -\dfrac{dx_A}{N_A - x_A (N_A + N_B)} \end{align}\]

Deriving the General Solution (II)

  • L.H.S.

\[ \int_{z_1}^{z_2} \frac{dz}{D_{AB} c_T} = \frac{(z_2 - z_1)}{D_{AB} c_T} \]

  • R.H.S.

Using substitution \(u = N_A - x_A (N_A + N_B)\), \(d u = -(N_A + N_B)\,dx_A\)

\[\begin{align} \int_{x_{A1}}^{x_{A2}} -\dfrac{dx_A}{N_A - x_A (N_A + N_B)} &= - \cdot - \frac{1}{N_A + N_B} \ln\!\left[N_A - x_A (N_A + N_B)\right] \bigg\vert_{x_{A1}}^{x_{A2}} \\ &= \frac{1}{N_A + N_B} \ln\!\left[\dfrac{ N_A - x_{A2} (N_A + N_B)} {N_A - x_{A1} (N_A + N_B)} \right] \end{align}\]

Deriving the General Solution (III)

We want to solve for \(N_A\)

\[\begin{align} \frac{(z_2 - z_1)}{c_T D_{AB}} &= \frac{1}{N_A + N_B} \ln\!\left[\dfrac{ N_A - x_{A2} (N_A + N_B)} {N_A - x_{A1} (N_A + N_B)} \right] \\ N_A &= \frac{c_T D_{AB}}{(z_2 - z_1)} \frac{N_A}{N_A + N_B} \ln\!\left[\dfrac{ N_A - x_{A2} (N_A + N_B)} {N_A - x_{A1} (N_A + N_B)} \right] \end{align}\]

We can gather all \(N_A / (N_A + N_B)\) in the R.H.S since it’s a constant

\[\begin{align} \boxed{ N_A = \frac{ c_T D_{AB}}{(z_2 - z_1)} \left(\frac{N_A}{N_A + N_B}\right) \% \ln\!\left[ \dfrac{\frac{N_A}{N_A + N_B} - x_{A2}} {\frac{N_A}{N_A + N_B} - x_{A1}} \right] } \end{align}\]
  • This is the general solution for binary gas transport.
  • Also works for \(N_A = -N_B\) (EMCD), with a little bit trick

Relation Between Gen. Sol. and EMCD

The general solution is not applicable \(N_B = -N_A\), but we can prove \(N_B / N_A \to -1\) reduces to the EMCD equation.

  • Let \(s = N_A / (N_A + N_B)\), so \(s \to \infty\) when \(N_B/N_A \to -1\)
  • Use the Taylor expansion that \(\lim_{u \to 0} \ln(1-u) = -u\)
\[\begin{align} \lim_{s \to \infty} \left(\frac{N_A}{N_A + N_B}\right) \ln\!\left[ \dfrac{ \frac{N_A}{N_A + N_B} - x_{A2}} {\frac{N_A}{N_A + N_B} - x_{A1} } \right] &= s \ln\!\left(\frac{s - x_2}{s - x_1}\right) \\ &= s \ln\!\left(\frac{1 - x_2/s}{1 - x_1/s}\right) \\ &= s [(-\frac{x_2}{s}) - (-\frac{x_1}{s})] \\ &= x_1 - x_2 \end{align}\]

This is the EMCD result!

Three Forms of Gass Mass Transport Equations (I)

In \(c_A\) form

  • Case 1: EMCD
    • \(N_A + N_B = 0\) \[ N_A = \dfrac{D_{AB}}{(z_2 - z_1)}(c_{A1} - c_{A2}) \]
  • Case 2: stagnant B
    • \(N_B = 0\)
    \[ N_A = \frac{D_{AB} c_T }{(z_2 - z_1)} \ln\! \left( \frac{1 - \frac{c_{A2}}{c_T} } {1-\frac{c_{A1}}{c_T}} \right) \]

  • General solution

    • \(N_B = k N_A\)

\[ N_A = \frac{D_{AB} c_T}{(z_2 - z_1)} \frac{N_A}{N_A + N_B} \ln\!\left[\dfrac{ \frac{N_A}{N_A + N_B} - \frac{c_{A2}}{c_T}} {\frac{N_A}{N_A + N_B} - \frac{c_{A1}}{c_T}} \right] \]

Three Forms of Gass Mass Transport Equations (II)

In \(x_A\) form

  • Case 1: EMCD
    • \(N_A + N_B = 0\) \[ N_A = \dfrac{D_{AB} c_T}{(z_2 - z_1)}(x_{A1} - x_{A2}) \]
  • Case 2: stagnant B
    • \(N_B = 0\)
    \[ N_A = \frac{D_{AB} c_T }{(z_2 - z_1)} \ln\! \left( \frac{1 - x_{A2} } {1- x_{A1}} \right) \]

  • General solution

    • \(N_B = \lambda N_A\)

\[ N_A = \frac{D_{AB} c_T}{(z_2 - z_1)} \frac{N_A}{N_A + N_B} \ln\!\left[\dfrac{ \frac{N_A}{N_A + N_B} - x_{A2}} {\frac{N_A}{N_A + N_B} - x_{A1}} \right] \]

Three Forms of Gass Mass Transport Equations (III)

In \(p_A\) form (ideal gas)

  • Case 1: EMCD
    • \(N_A + N_B = 0\) \[ N_A = \dfrac{D_{AB}}{RT(z_2 - z_1)}(p_{A1} - p_{A2}) \]
  • Case 2: stagnant B
    • \(N_B = 0\)
    \[ N_A = \frac{D_{AB} p_T}{RT(z_2 - z_1)} \ln\! \left( \frac{p_T - p_{A2}} {p_T - p_{A1}} \right) \]

  • General solution

    • \(N_B = \lambda N_A\)

\[ N_A = \frac{D_{AB} p_T}{RT(z_2 - z_1)} \frac{N_A}{N_A + N_B} \ln\!\left[\dfrac{ \frac{N_A}{N_A + N_B} - x_{A2}} {\frac{N_A}{N_A + N_B} - x_{A1}} \right] \]

General Solution – \(x_A(z)\) Profile

In all the cases we study the S.S. condition:

\[\frac{d N_A}{d z} = 0\]

For the general case \(s = N_A / (N_A + N_B)\), we have

\[\begin{align} \frac{dN_A}{dz} &= \frac{d}{dz} \left[ \frac{D_{AB} c_T}{s - x_A} \frac{d x_A}{d z}\right] = 0\\ \frac{D_{AB} c_T}{s - x_A} \frac{d x_A}{d z} &= \mathrm{Const} \end{align}\]

\(x_A(z)\) has a general solution with exponential form (with \(K_1\) and \(K_2\) being constants)

\[\begin{align} \boxed{ x_{A} = s - K_1 e^{K_2 z} } \end{align}\]

\(x_A(z)\) Profile

Notes on the Relation Between \(N_A\) and \(N_B\) (1)

Using steady state condition, we need to know relation between \(N_A\) and \(N_B\) before solving the general EQ.

It depends on the system setup and mass balance.

Let’s consider the same chemical reaction of hydrogen dissociation by a solid catalst

\[\begin{align} \text{H}_2\ (A, \text{gas}) \rightarrow 2\text{H}^*\ (B, \text{gas}) \end{align}\]

  • Case 1: reaction through a solid catalyst at bottom of a tube

    • The flux of A and B have opposite signs
    • \(N_B = -2 N_A\)

Notes on the Relation Between \(N_A\) and \(N_B\) (2)

  • Case 2: gas flow through a solid catalyst inside a tube

    • The flux of A and B have the same sign
    • \(N_B = 2 N_A\)

Take home question: - How do the flux directions affect the general solution?

Measuring Diffusivity \(D_{AB}\) In Gases

  • Several experimental methods exist for gases, evaporated liquid and sublimated solids (see Geankoplis Ch 6.2E)
  • We will introduce the two-bulb method for gases
  • Typical setup see Duncan & Toor AIChE J. 1962, 8, 38-41
  • Which case should we apply?

Two-Bulb Experiment: Conditions

Conditions for the two-bulb experiment

  • Initially, pure A in bulb 1 and pure B and bulb 2
  • \(t=0\), the valve is opened slowly to minimize convection
  • \(t=t_e\), the valve is closed and the composition in 1 and 2 are analyzed
  • The valve open time is much shorter than \(t_2 - t_1\)
  • The tube is a very thin capillary 👉 no convection
  • Constant \(p_T\) and \(T\) throughout experiment

Two-Bulb Experiment: Pseudo Steady State

We can apply:

  • EMCD condition (no convection)
  • Pseudo-steady state (P.S.S) assumption
    • At each time step, we assume \(N_A\) or \(J_{Az}^*\) is constant (linear \(c_A\) profile)
    • But net \(N_A\) flux accumulates A molecules in bulb 2
    • \(c_A\) in bulb 2 changes over time

Two-Bulb Experiment: Governing Equations

We use the mass balance of the system

\[\begin{align*} \text{[Mass In]} &= \text{[Accumulation]} \\ S \cdot J_{Az}^* &= V_2 \frac{d c_{A2}}{dt} \\ D_{AB} \frac{c_{A1} - c_{A2}}{L} \cdot S &= V_2 \frac{d c_{A2}}{dt} \end{align*}\]

Since the total pressure \(p_T\) is constant, the average concentration of \(c_A\) in the system, \(c_{A, av}\) is also constant

\[\begin{align*} V_T c_{A, av} &= (V_1 + V_2)c_{A, av} \\ &= V_1c_{A1}(t=0) + V_2c_{A2}(t=0) \\ &= V_1c_{A1}(t\neq0) + V_2c_{A2}(t\neq0) \end{align*}\]

Two-Bulb Experiment: Solutions

We are interested in \(c_{A2}\), so substitute \(c_{A1}\) with relation to \(c_{A, av}\):

\[ c_{A1} = \frac{V_T c_{A, av} - V_2 c_{A2}}{V_1} \]

After the substitution, rearrangement and integration we get:

\[\begin{align*} \ln\!\left[ \frac{c_{A, av} - c_{A2}(t=t_e)}{c_{A, av} - c_{A2}(t=0)} \right] &= -\frac{D_{AB} V_T S}{V_1 V_2 L} \cdot t \\ \end{align*}\]

We can extract \(D_{AB}\) usingt the slope of the plot!

Some Typical Diffusivity Measurements

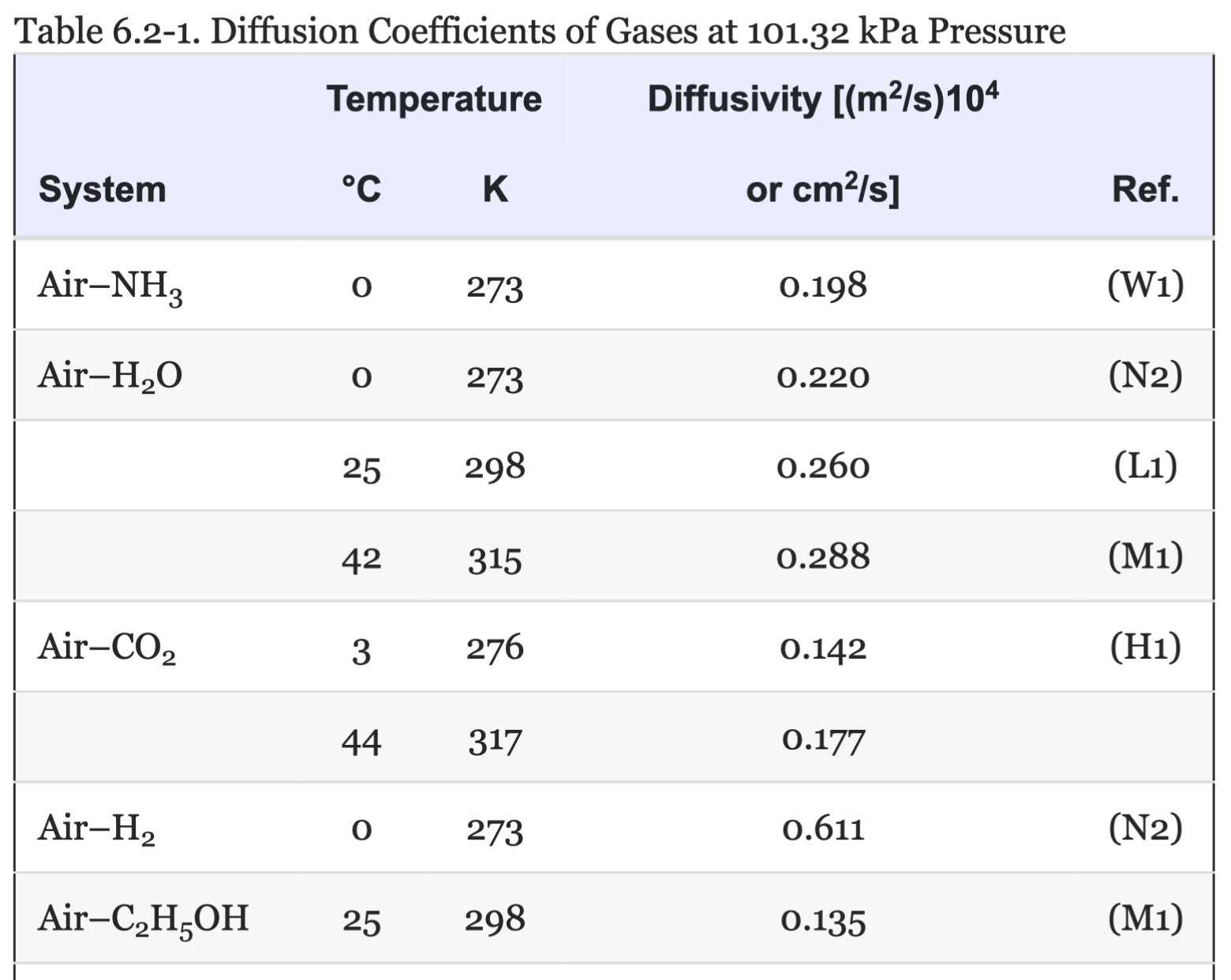1

Summary

  • General solution for \(N_B = k N_A\)
  • Like stagnant B case, general solution take a logarithm form for \(N_A\)
  • When \(x_{A1}\) and \(x_{A_2}\) are determined, the flux \(N_A\) is controlled by the relation between \(N_B\) and \(N_A\)
  • The ratio between \(N_B\) and \(N_A\) depends on the system and setup
  • Diffusivity \(D_{AB}\) can be determined by EMCD through two-bulb setup

Preview of Next Class: Theories for predicting \(D_{AB}\)

  • Kinetic theory

\[ D_{AB} = \frac{1}{3} \overline{u} \lambda \]

  • Chapman-Enskog theory

\[ D_{AB} \propto \frac{T^{\frac{3}{2}}}{P} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \]

  • Fuller method

\[ D_{AB} \propto \frac{T^{1.75}}{P} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \]