CHE 318 Lecture 04

Molecular Diffusivity: Theories and Measurement

Dr. Tian Tian

2026-01-12

Note

  • Course Website Updated!

https://tiangroup-uofa.github.io/che318-mass-transfer/

QR Code

Recap

  • General solution for diffusion binary mixture gas systems (\(N_B = k N_A\))
    • \(k = -1\) reduces to EMCD solution
    • Total flux \(N_A\) is EMCD flux times a coefficient
\[\begin{align} N_A = \frac{ c_T D_{AB}}{(z_2 - z_1)} \left(\frac{N_A}{N_A + N_B}\right) \ln\!\left[\dfrac{ \frac{N_A}{N_A + N_B} - x_{A2}} {\frac{N_A}{N_A + N_B} - x_{A1}} \right] \end{align}\]
  • Brief discussion about diffusivity measurement: two-bulb setup

Demonstration of General Solution

Interaction Time!

participation link

Results and comments to be published after the class

Convection-Driven Flux Change

Figure 1

Learning Outcomes

After today’s lecture, you will be able to:

  • Recall multiple theories of molecular diffusivity
  • Analyze the diffusivity \(D_{AB}\) as function of \((T, P)\)
  • Derive new diffusivity values from standard table
  • Formulate governing equations for different scenarios measuring the diffusivity

Let’s Look At The General Mass Transfer Equation (Again)

\[ N_A = \frac{D_{AB} c_T}{(z_2 - z_1)} s \ln\!\left[\dfrac{ s - \frac{c_{A2}}{c_T}} {s - \frac{c_{A1}}{c_T}} \right] \quad s = \frac{N_A}{N_A + N_B} \]

What values do we know from the system setup?

  • Geometry: \(z_1\), \(z_2\), \(c_{A1}\), \(c_{A2}\), \(c_T\)
  • Chemical reaction stoichiometry: \(k\)

What else value(s) do we need to solve \(N_A\)?

  • \(D_{AB}\): generally \(D_{AB}(z) = \text{Const}\)
  • But \(D_{AB}=f(T, P, \cdots)\)

Motivation to Have Theory About Diffusivity

  • Solving the general solution for gas mass transfer requires parameter \(D_{AB}\) (and \(D_{BA}\))!
  • Measuring every \(D_{AB}\) pair for gases is tedious
  • \(D_{AB}\) is dependent on conditions \(T, P\)
  • We need to have theories that can predict diffusivity \(D_{AB}\) without doing all pair experiments and all \((T, P)\) conditions!
  • In the lease case, the theory should allow extrapolating a measured \(D_{AB}(T_1, P_1)\) to \(D_{AB}(T_2, P_2)\)

Molecular Diffusivity Theory – Kinetic Theory

In dilute gas regime (\(p_T \approx \text{atm}\)), the kinetic behaviour of gas molecules can be described using kinetic theory. A few assumptions are made:

  1. Interdiffusion between A and B are dominated by collision between molecules (low \(p_T\) 👉 only 2 molecules can collide at the same time)
  2. The molecules are rigid spheres having particle masses \(m_A\), \(m_B\) and diameters \(d_A\) and \(d_B\)

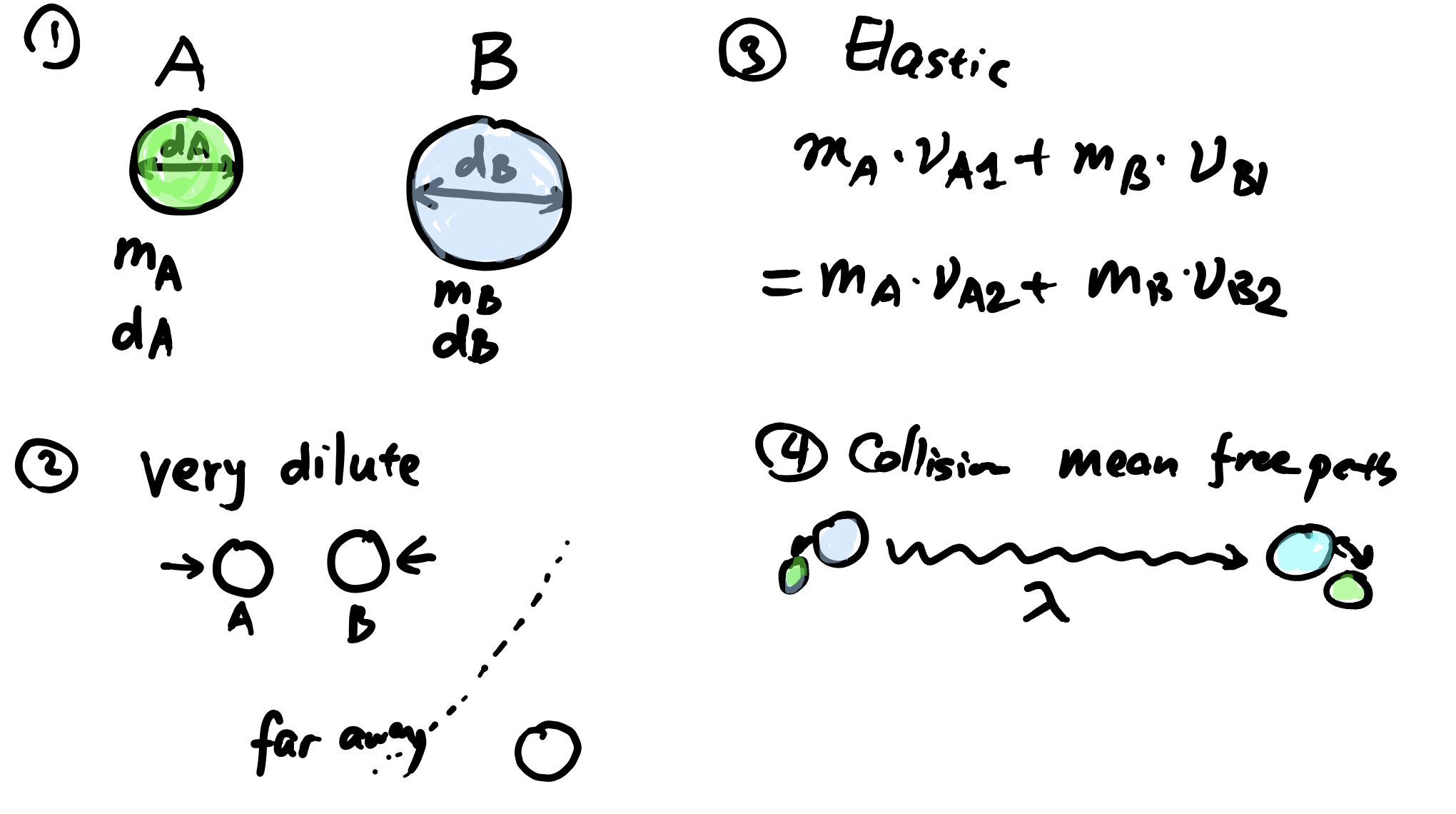
Scheme of gas kinetic theory

Kinetic Theory – Key Results

There are some results from the kinetic theory: 1

  1. Mean molecular speed \(\overline{u}\) \[ \overline{u} = \sqrt{\frac{8 k_B T}{\pi \overline{m_{AB}}}} \]

  2. Mean free path (between collisions): \(\lambda_{A,B}\) \[ \lambda_{AB}=\frac{1}{\sqrt{2} \pi d_{AB}^2 c_T} \]

  1. Frequency of molecule A colliding with wall (\(Z\), unit \(\text{m}^{-2}\cdot \text{s}^{-1}\)): \[ Z_A = \frac{1}{4} c_A \overline{u} \]

where \(d_{AB} = \frac{d_A + d_B}{2}\), \(m_{AB}^{-1} = m_{A}^{-1} + m_B^{-1}\), \(k_B\) is the Boltzmann constant

  1. We also have the average distance \(a\) to one plane from last collision: \[ a = \frac{2}{3}\lambda_{AB} \]

Kinetic Theory – Mass Transfer

When there is only molecular diffusion (no convection), at plane \(z=0\), the flux can be described by:

\[\begin{align} J_{Az}^*\vert_{z=0} &= \text{[In]}\vert_{z=-a} - \text{[Out]}\vert_{z=+a} \\ &= \frac{1}{4} c_T [x_A \overline{u}]\vert_{z=-a} \\ &- \frac{1}{4} [c_T x_A \overline{u}]\vert_{z=+a}\\ &= -\frac{1}{4} c_T \cdot 2a \cdot \overline{u} \frac{d x_A}{dz} \\ &= -D_{AB} c_T \frac{dx_A}{dz} \end{align}\]

We can now link \(D_{AB}\) to microscopic properties!

Mass balance in gas kinetic theory

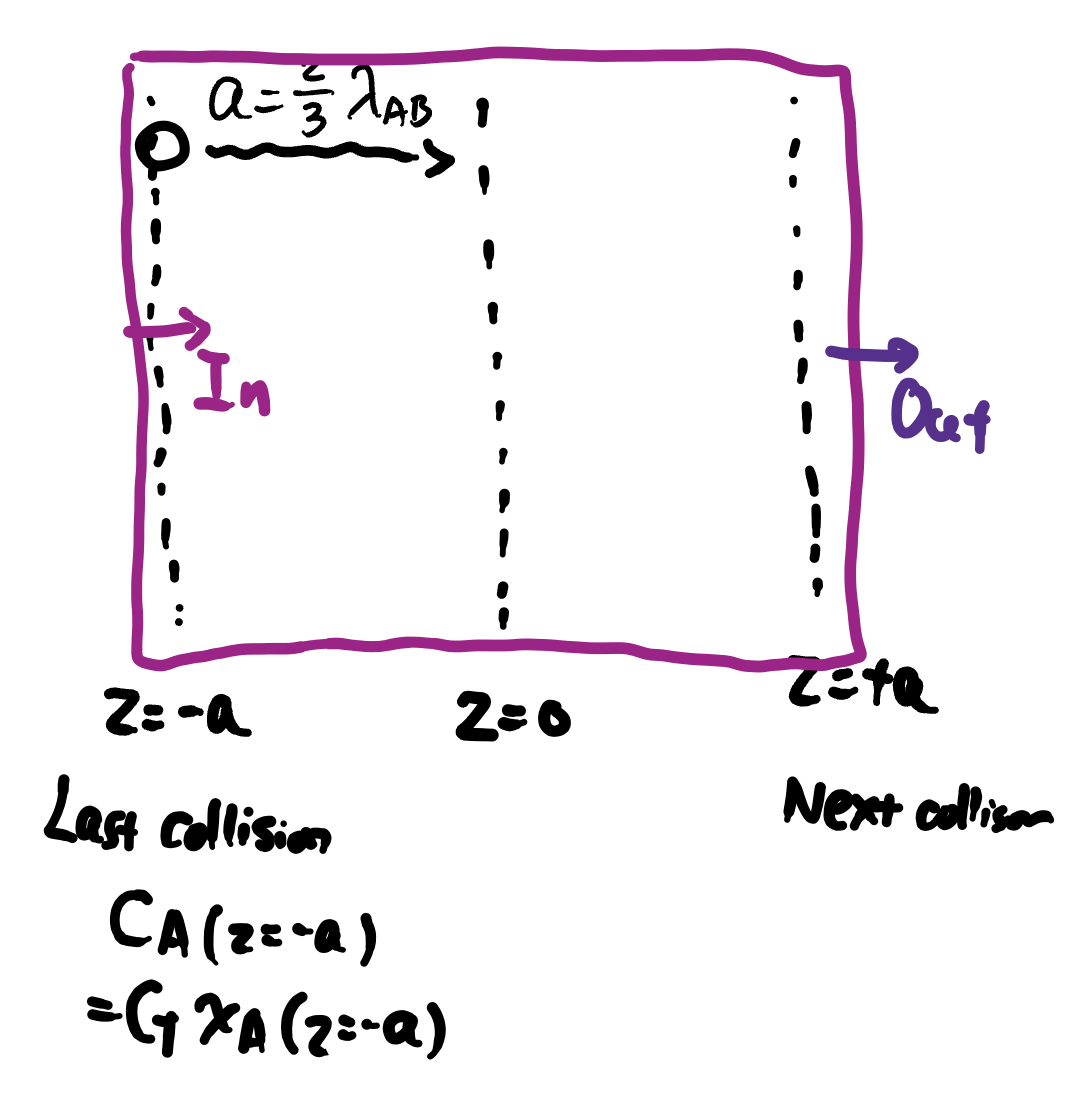
Kinetic Theory of Diffusivity – Conclusion

Results:

\[ D_{AB} = \frac{1}{3} \overline{u} \lambda_{A,B} \]

  • \(\overline{u}\): average molecular velocity
  • \(\lambda\): mean free path between collisions

Assumptions:

  • Rigid sphere type molecules (what are they?)
  • No interaction upon collisions
  • Collisions are elastic (momentum conserved)
  • Good for dilute gases (low \(P\))
  • Not accurate otherwise

Molecular Diffusivity – Chapman-Enskog Theory

We can take real interaction between molecules into the kinetic theory!

\[\begin{align} D_{AB} &= \frac{1.8583\times{}10^{-7} T^{3/2}} {p_T \sigma_{AB}^2 \Omega_{D, AB}} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\ &\propto \frac{T^{\frac{3}{2}}}{p_T} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \end{align}\]
  • \(m_A\), \(m_B\), molecular weight
  • \(\sigma_{AB}\): average collision radius between A and B
  • \(\Omega_{D, AB}\): Lennard-Jones collision integral
    • \(\Omega_{D, AB}=1\) for elastic collision
    • Chapman-Enskog theory accounts for non-elastic collision using \(\Omega_{D, AB}\neq1\)

Chapman-Enskog Theory: How to Use

\[\begin{align} D_{AB} = \frac{1.8583\times{}10^{-7} T^{3/2}} {p_T \sigma_{AB}^2 \Omega_{D, AB}} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \end{align}\]

The Chapman-Enskog theory formula in Geankoplis book need to use the following units:

  • \(T\): absolute temperature in \(\text{K}\)
  • \(m_A\), \(m_B\): molecular weight in \(\text{kg} \cdot (\text{kg mol})^{-1}\) or \(\text{g} \cdot (\text{g mol})^{-1}\)
  • \(p_T\): absolute pressure in \(\text{atm}\)
  • \(\sigma_{AB}\): average collision diameter in Å
  • \(\Omega_{D, AB}\): collision integral (dimensionless)

Resulting \(D_{AB}\) is in \(\text{m}^2 \cdot \text{s}^{-1}\)

Chapman-Enskog Theory & Lennard Jones Potential

  • Parameters \(\sigma_{AB}\) and \(\Omega_{D, AB}\) can be derived using Lennard-Jones (LJ) potential
  • LJ potential described the interaction energy \(U_{AB}\) between 2 molecules at distance \(r\) follows:
\[\begin{align} U_{AB}(r) = 4\epsilon_{AB}\left[ (\frac{\sigma_{AB}}{r})^{12} - (\frac{\sigma_{AB}}{r})^{6} \right] \end{align}\]

How to get the parameters from table:

  • \(\sigma_{AB} = (\sigma_{A} + \sigma_{B})/2\)
  • \(\epsilon_{AB} = \sqrt{\epsilon_A \epsilon_B}\)
  • \(\Omega_{D, AB}\): get interpolated table values as function of \(T^*=k_B T / \epsilon_{AB}\)

Note

Check online course materials for the \(\Omega_{D, AB}\) table!

Molecular Diffusivity Theory – Fuller Method

The Chapman Enskog theory can be difficult to use, engineers need some simplied empirical rules.

\[\begin{align} D_{AB} &= \frac{1.0\times{}10^{-7} T^{1.75} }{p_T \left[ (\sum \nu_A)^{1/3} + (\sum \nu_B)^{1/3}\right]^2} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\ &\propto \frac{T^{1.75}}{p_T} \end{align}\]
  • Mainly to overcome the complicated estimation of \(\Sigma_{D, AB}\) in Chapman-Enskog Theory
  • \(\sum \nu_i\) sum of structural volume increments
  • \(\sum \nu_i\) can be estimated from individual atoms
  • Easier to use than the Chapman-Enskog Theory, but less accurate

Fuller Method: How to Use

\[\begin{align} D_{AB} = \frac{1.0\times{}10^{-7} T^{1.75} }{p_T \left[ (\sum \nu_A)^{1/3} + (\sum \nu_B)^{1/3}\right]^2} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \end{align}\]

The Fuller method formula in Geankoplis book need to use the following units:

  • \(T\): absolute temperature in \(\text{K}\)
  • \(m_A\), \(m_B\): molecular weight in \(\text{kg} \cdot (\text{kg mol})^{-1}\) or \(\text{g} \cdot (\text{g mol})^{-1}\)
  • \(p_T\): absolute pressure in \(\text{atm}\)
  • \(\nu_{A}\), \(\nu_{B}\): structural volume increments (dimensionless)

Resulting \(D_{AB}\) is in \(\text{m}^2 \cdot \text{s}^{-1}\)

How to Use the Fuller Method From a Table

We need to determine \(\sum \nu_A\) and \(\sum \nu_B\), Check Table 6.2-2 of Geankoplis 4th ed.

  • \(\sum \nu_i\) are dimensionless numbers
  • For known gases in the table, use its value in the table
    • Air: \(\nu = 20.1\)
    • O\(_2\): \(\nu = 16.6\)
  • For an unknown gas, use its chemical composition
    • For chemical formula \(\text{C}_x \text{H}_y \text{O}_z\), \[ \sum \nu(\text{C}_x \text{H}_y \text{O}_z) = \nu(\text{C}) \cdot x + \nu(\text{H}) \cdot y + \nu(\text{O}) \cdot z \]

Estimating \(D_{AB}\) At Different \((T, P)\)

For the same pair of (A, B), both the Chapman-Enskog and Fuller methods have the same form \[ D_{AB} \propto \frac{T^n}{P} \]

This means we can find one existing \(D_{AB}\) value from table and extrapolate: \[ \frac{D_{AB}\vert_1}{D_{AB}\vert_2} = \left(\frac{T_1}{T_2}\right)^{n} \left( \frac{P_2}{P_1} \right) \]

Fuller method is often used in chemical engineering, where \(n=1.75\).

Example 1: Chapman-Enskog Theory vs Fuller Method

Question: calculate the diffusivity \(D_{AB}\) for methan–ethan system at 313 K and 1 atm.

Chapman-Enskog Theory

  • \(m_A=16.04\), \(m_B=30.07\)
  • \(\rho_A (Å)=3.822\), \(\rho_B (Å)=4.418\)
  • \(\epsilon_A = k_B * (137\ \text{K})\), \(\epsilon_B = k_B * (230\ \text{K})\)
  • \(\Omega_{D, AB} = 1.125\) in this case

Fuller Method

  • \(m_A=16.04\), \(m_B=30.07\)
  • \(\nu(\text{C})=16.5\), \(\nu(\text{H})=1.98\)

The experimental value at this condition is \(D_{AB}=1.84\times 10^{-5}\ \text{m}^2\cdot s^{-1}\). Compare the percent errors in both methods.

Summary

  • Diffusivity \(D_{AB}\) value is the key to solve the transport problem in gases
  • \(D_{AB}\) can be measured from experiments, but not exhaustively
  • Several theories predict the value for \(D_{AB}\) with certain accuracy
  • Chapman-Enkog theory and Fuller method both have \(D_{AB}\propto T^n/P\) form
  • Fuller method more often used as it can approximate \(D_{AB}\) solely by taking values from table