- Diffusivity (m^2/s) = 1.666e-05
- Percentage error: 9.45%
- Diffusivity (m^2/s) = 1.728e-05
- Percentage error: 6.07%
Molecular Diffusivity: Theories and Measurement
Dr. Tian Tian
January 12, 2026
Results and comments to be published after the class
Advanced topic, not shown in presentation
The ratio between total flux in general solution \(N_A(\text{gen})\) and \(N_A(\text{EMCD})\) can be written as:
\[\begin{align} \frac{N_A(\text{gen})}{N_A(\text{EMCD})} &= \frac{s \ln\! \left[ \frac{s - x_{A2}}{s - x_{A1}} \right]}{x_{A1} - x_{A2}} \\ &= \frac{s \ln\! \left[ \frac{s - x_{A2}}{s - x_{A1}} \right]}{(s - x_{A2}) - (s - x_{A1})} \\ &= \frac{s}{\text{LM}(s-x_A)} \end{align}\]where \(\text{LM}(u)\) is the log-mean function (similar treatment in Lecture 2), and \(s = N_A / (N_A + N_B)\).
There are several limiting cases. Let’s assume \(x_{A1} > x_{A2}\) for simplicity, and there is a real solution to the \(N_A(\text{gen})\)
\(s > x_{A1}\):
\(s - x_{A1}\) and \(s - x_{A2}\) must be both positive to ensure a solution. Therefore \(\text{LM}(s-x_A) < s\). We know that \(N_A(\text{gen})>N_A(\text{EMCD})\).
Example: diffusion through stagnant B (\(s = 1\))
In this case \(\text{LM}(s-x_A) = \text{LM}(x_B)\), we can conclude that the diffusion through stagnant B case always enhances total flux compared with EMCD.
A signature of such transport is the \(x_A(z)\) profile is concave, as shown in Figure 1 (a).
\(s < 0\):
\(s - x_{A2}\) and \(s - x_{A1}\) are be both negative. Therefore \(|\text{LM}(s-x_A)| > s\). We know that \(N_A(\text{gen})<N_A(\text{EMCD})\), but \(N_A\) is still positive.
Example: counter \(N_B\) flux (\(N_B/N_A < -1\))
The opposite direction of \(N_B\) attenuates the molar flux of A. A signature of such transport is the \(x_A(z)\) profile is convex, as shown in Figure 1 (b).
\(0 < s < x_2\):
\(s - x_{A2}\) and \(s - x_{A1}\) are be both negative. Since \(s >0\), we actually can have \(N_A < 0\)!
Such situation may be counter-intuitive but the solution is physically valid, as the only solution to satisfy such criteria is \(N_B < 0\) and \(N_A < 0\) at the same time. As we cannot directly compare \(s\) and \(\text{LM}(s-x_A)\) in this case, \(|N_A(\text{gen})|\) can be either smaller or larger than \(N_A(\text{EMCD})\), as shown in Figure 1 (c) and (d).
\(x_2 < s < x_1\):
The expression inside the logarithm is negative and we do not have a real solution to the general equation for \(N_A\).
After today’s lecture, you will be able to:
\[ N_A = \frac{D_{AB} c_T}{(z_2 - z_1)} s \ln\!\left[\dfrac{ s - \frac{c_{A2}}{c_T}} {s - \frac{c_{A1}}{c_T}} \right] \quad s = \frac{N_A}{N_A + N_B} \]
What values do we know from the system setup?
What else value(s) do we need to solve \(N_A\)?
In dilute gas regime (\(p_T \approx \text{atm}\)), the kinetic behaviour of gas molecules can be described using kinetic theory. A few assumptions are made:
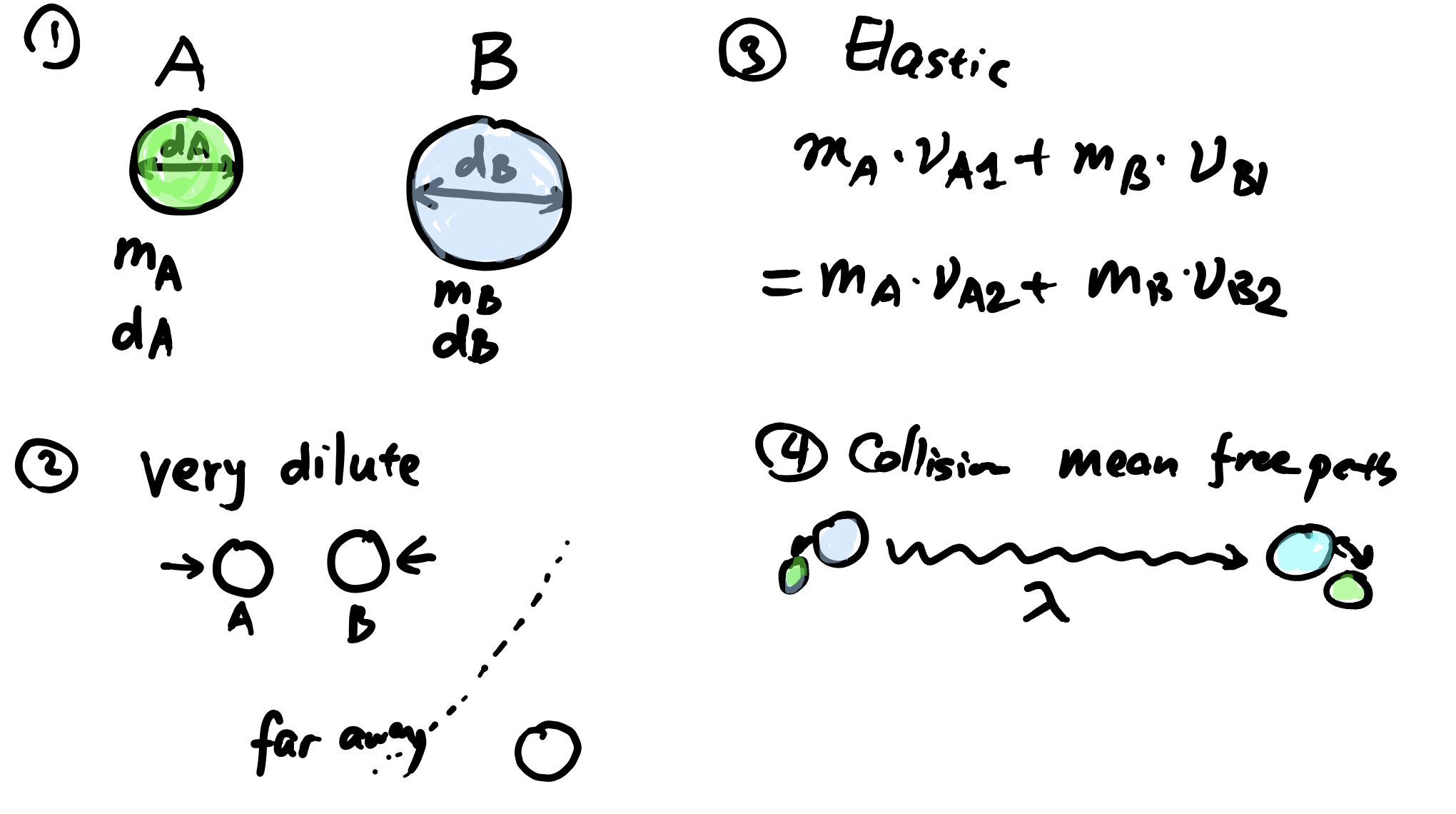
There are some results from the kinetic theory: 1
Mean molecular speed \(\overline{u}\) \[ \overline{u} = \sqrt{\frac{8 k_B T}{\pi \overline{m_{AB}}}} \]
Mean free path (between collisions): \(\lambda_{A,B}\) \[ \lambda_{AB}=\frac{1}{\sqrt{2} \pi d_{AB}^2 c_T} \]
where \(d_{AB} = \frac{d_A + d_B}{2}\), \(m_{AB}^{-1} = m_{A}^{-1} + m_B^{-1}\), \(k_B\) is the Boltzmann constant
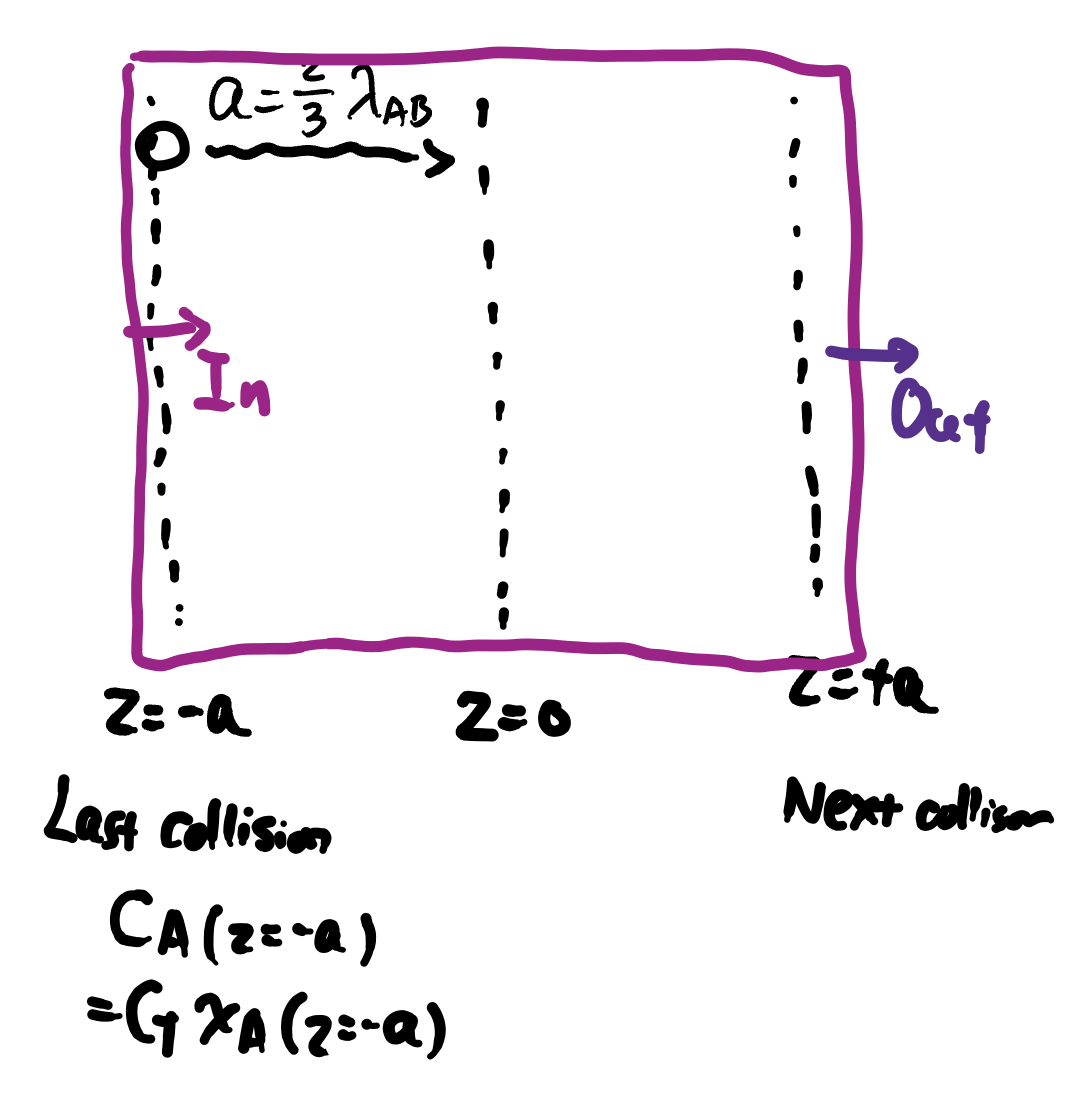
When there is only molecular diffusion (no convection), at plane \(z=0\), the flux can be described by:
We can now link \(D_{AB}\) to microscopic properties!
Results:
\[ D_{AB} = \frac{1}{3} \overline{u} \lambda_{A,B} \]
Assumptions:
We can take real interaction between molecules into the kinetic theory!
\[\begin{align} D_{AB} &= \frac{1.8583\times{}10^{-7} T^{3/2}} {p_T \sigma_{AB}^2 \Omega_{D, AB}} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\ &\propto \frac{T^{\frac{3}{2}}}{p_T} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \end{align}\]The Chapman-Enskog theory formula in Geankoplis book need to use the following units:
Resulting \(D_{AB}\) is in \(\text{m}^2 \cdot \text{s}^{-1}\)
How to get the parameters from table:
Check online course materials for the \(\Omega_{D, AB}\) table!
The Chapman Enskog theory can be difficult to use, engineers need some simplied empirical rules.
\[\begin{align} D_{AB} &= \frac{1.0\times{}10^{-7} T^{1.75} }{p_T \left[ (\sum \nu_A)^{1/3} + (\sum \nu_B)^{1/3}\right]^2} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\ &\propto \frac{T^{1.75}}{p_T} \end{align}\]The Fuller method formula in Geankoplis book need to use the following units:
Resulting \(D_{AB}\) is in \(\text{m}^2 \cdot \text{s}^{-1}\)
We need to determine \(\sum \nu_A\) and \(\sum \nu_B\), Check Table 6.2-2 of Geankoplis 4th ed.
For the same pair of (A, B), both the Chapman-Enskog and Fuller methods have the same form \[ D_{AB} \propto \frac{T^n}{P} \]
This means we can find one existing \(D_{AB}\) value from table and extrapolate: \[ \frac{D_{AB}\vert_1}{D_{AB}\vert_2} = \left(\frac{T_1}{T_2}\right)^{n} \left( \frac{P_2}{P_1} \right) \]
Fuller method is often used in chemical engineering, where \(n=1.75\).
Question: calculate the diffusivity \(D_{AB}\) for methan–ethan system at 313 K and 1 atm.
The experimental value at this condition is \(D_{AB}=1.84\times 10^{-5}\ \text{m}^2\cdot s^{-1}\). Compare the percent errors in both methods.
adapted from BSL Transport Phenomena ch 17.3↩︎
---
title: "CHE 318 Lecture 04"
subtitle: "Molecular Diffusivity: Theories and Measurement"
author: "Dr. Tian Tian"
date: "2026-01-12"
format:
html: {}
revealjs:
output-file: slides.html
pdf:
output-file: L04.pdf
---
::: {.content-visible when-format="html" unless-format="revealjs"}
::: {.callout-note}
- Slides 👉 [Open presentation🗒️](./slides.html)
- PDF version of course note 👉 [Open in pdf](./L04.pdf)
- Handwritten notes 👉 [Open in pdf](./public/L04_annotated.pdf)
:::
:::
::: {.content-visible when-format="revealjs"}
::: {.callout-note}
- **Course Website Updated!**
[https://tiangroup-uofa.github.io/che318-mass-transfer/](https://tiangroup-uofa.github.io/che318-mass-transfer/)
<div style="width: 100%; text-align: center;">
<img
src="https://quickchart.io/qr?text=https://tiangroup-uofa.github.io/che318-mass-transfer/&size=250"
alt="QR Code"
style="width: 150px; height: 150px; display: block; margin: 0 auto;"
/>
</div>
:::
:::
## Recap
- **General solution** for diffusion binary mixture gas systems ($N_B = k N_A$)
- $k = -1$ reduces to EMCD solution
- Total flux $N_A$ is EMCD flux times a coefficient
```{=tex}
\begin{align}
N_A = \frac{ c_T D_{AB}}{(z_2 - z_1)}
\left(\frac{N_A}{N_A + N_B}\right)
\ln\!\left[\dfrac{
\frac{N_A}{N_A + N_B} - x_{A2}}
{\frac{N_A}{N_A + N_B} - x_{A1}}
\right]
\end{align}
```
- Brief discussion about diffusivity measurement: two-bulb setup
## Demonstration of General Solution
```{=html}
<iframe width="100%" height="800"
src="../../scripts/L03_xa_profile.html" title="Webpage example"></iframe>
```
## Interaction Time!
[participation link](https://app.wooclap.com/318L04?from=instruction-slide)
*Results and comments to be published after the class*
::: {.content-visible when-format="revealjs"}
---
## Convection-Driven Flux Change
{#fig-na-comp width="100%"}
:::
::: {.content-visible when-format="html" unless-format="revealjs"}
---
## Detailed Explanation for Convection-Driven Flux Change
::: {.callout-note}
Advanced topic, not shown in presentation
:::
The ratio between total flux in general solution $N_A(\text{gen})$ and $N_A(\text{EMCD})$ can be written as:
```{=tex}
\begin{align}
\frac{N_A(\text{gen})}{N_A(\text{EMCD})}
&= \frac{s \ln\! \left[
\frac{s - x_{A2}}{s - x_{A1}}
\right]}{x_{A1} - x_{A2}} \\
&= \frac{s \ln\! \left[
\frac{s - x_{A2}}{s - x_{A1}}
\right]}{(s - x_{A2}) - (s - x_{A1})} \\
&= \frac{s}{\text{LM}(s-x_A)}
\end{align}
```
where $\text{LM}(u)$ is the log-mean function (similar treatment in [Lecture 2](../L02)), and $s = N_A / (N_A + N_B)$.
There are several limiting cases. Let's assume $x_{A1} > x_{A2}$ for simplicity, and there is a real solution to the $N_A(\text{gen})$
1. $s > x_{A1}$:
$s - x_{A1}$ and $s - x_{A2}$ must be both positive to ensure a
solution. Therefore $\text{LM}(s-x_A) < s$. We know that
$N_A(\text{gen})>N_A(\text{EMCD})$.
- Example: diffusion through stagnant B ($s = 1$)
In this case $\text{LM}(s-x_A) = \text{LM}(x_B)$, we can conclude that the diffusion through stagnant B case **always enhances** total flux compared with EMCD.
A signature of such transport is the $x_A(z)$ profile is **concave**, as shown in @fig-na-comp (a).
2. $s < 0$:
$s - x_{A2}$ and $s - x_{A1}$ are be both negative. Therefore $|\text{LM}(s-x_A)| > s$. We know that
$N_A(\text{gen})<N_A(\text{EMCD})$, but $N_A$ is still positive.
- Example: counter $N_B$ flux ($N_B/N_A < -1$)
The opposite direction of $N_B$ **attenuates** the molar flux of A. A signature of such transport is the $x_A(z)$ profile is **convex**, as shown in @fig-na-comp (b).
3. $0 < s < x_2$:
$s - x_{A2}$ and $s - x_{A1}$ are be both negative. Since $s >0$, we actually can have $N_A < 0$!
Such situation may be counter-intuitive but the solution is physically valid, as the only solution to satisfy such criteria is $N_B < 0$ and $N_A < 0$ at the same time.
As we cannot directly compare $s$ and $\text{LM}(s-x_A)$ in this case, $|N_A(\text{gen})|$ can be either smaller or larger than $N_A(\text{EMCD})$, as shown in @fig-na-comp (c) and (d).
4. $x_2 < s < x_1$:
The expression inside the logarithm is negative and we do not have a real solution to the general equation for $N_A$.
{#fig-na-comp width="100%"}
:::
---
## Learning Outcomes {.center}
After today's lecture, you will be able to:
- **Recall** multiple theories of molecular diffusivity
- **Analyze** the diffusivity $D_{AB}$ as function of $(T, P)$
- **Derive** new diffusivity values from standard table
- **Formulate** governing equations for different scenarios measuring the diffusivity
---
## Let's Look At The General Mass Transfer Equation (Again)
$$
N_A = \frac{D_{AB} c_T}{(z_2 - z_1)}
s
\ln\!\left[\dfrac{
s - \frac{c_{A2}}{c_T}}
{s - \frac{c_{A1}}{c_T}}
\right]
\quad
s = \frac{N_A}{N_A + N_B}
$$
What values do we know from the system setup?
- Geometry: $z_1$, $z_2$, $c_{A1}$, $c_{A2}$, $c_T$
- Chemical reaction stoichiometry: $k$
What else value(s) do we need to solve $N_A$?
- $D_{AB}$: generally $D_{AB}(z) = \text{Const}$
- But $D_{AB}=f(T, P, \cdots)$
---
## Motivation to Have Theory About Diffusivity {.center}
- Solving the general solution for gas mass transfer requires parameter $D_{AB}$ (and $D_{BA}$)!
- Measuring every $D_{AB}$ pair for gases is tedious
- $D_{AB}$ is dependent on conditions $T, P$
- We need to have theories that can **predict** diffusivity $D_{AB}$ **without** doing all pair experiments and all $(T, P)$ conditions!
- In the lease case, the theory should allow extrapolating a measured $D_{AB}(T_1, P_1)$ to $D_{AB}(T_2, P_2)$
---
## Molecular Diffusivity Theory -- Kinetic Theory
In dilute gas regime ($p_T \approx \text{atm}$), the kinetic behaviour
of gas molecules can be described using kinetic theory. A few
assumptions are made:
1. Interdiffusion between A and B are dominated by **collision** between molecules (low $p_T$ 👉 **only 2** molecules can collide at the same time)
2. The molecules are rigid spheres having particle masses $m_A$, $m_B$ and diameters $d_A$ and $d_B$
{width="80%"}
## Kinetic Theory -- Key Results
There are some results from the kinetic theory:
^[adapted from *BSL Transport Phenomena ch 17.3*]
::: {.columns}
::: {.column width="50%"}
1. Mean molecular speed $\overline{u}$
$$
\overline{u} = \sqrt{\frac{8 k_B T}{\pi \overline{m_{AB}}}}
$$
2. Mean free path (between collisions): $\lambda_{A,B}$
$$
\lambda_{AB}=\frac{1}{\sqrt{2} \pi d_{AB}^2 c_T}
$$
:::
::: {.column width="50%"}
3. Frequency of molecule A colliding with wall ($Z$, unit $\text{m}^{-2}\cdot \text{s}^{-1}$):
$$
Z_A = \frac{1}{4} c_A \overline{u}
$$
where $d_{AB} = \frac{d_A + d_B}{2}$, $m_{AB}^{-1} = m_{A}^{-1} + m_B^{-1}$, $k_B$ is the Boltzmann constant
4. We also have the average distance $a$ to one plane from last collision:
$$
a = \frac{2}{3}\lambda_{AB}
$$
:::
:::
---
## Kinetic Theory -- Mass Transfer
When there is only molecular diffusion (no convection), at plane $z=0$, the flux can be described by:
::: {.columns}
::: {.column width="60&"}
```{=tex}
\begin{align}
J_{Az}^*\vert_{z=0} &= \text{[In]}\vert_{z=-a} - \text{[Out]}\vert_{z=+a} \\
&= \frac{1}{4} c_T [x_A \overline{u}]\vert_{z=-a} \\
&- \frac{1}{4} [c_T x_A \overline{u}]\vert_{z=+a}\\
&= -\frac{1}{4} c_T \cdot 2a \cdot \overline{u} \frac{d x_A}{dz} \\
&= -D_{AB} c_T \frac{dx_A}{dz}
\end{align}
```
We can now link $D_{AB}$ to microscopic properties!
:::
::: {.column width="40%"}
{width="80%"}
:::
:::
---
## Kinetic Theory of Diffusivity -- Conclusion
::: {.columns}
::: {.column width="50%"}
Results:
$$
D_{AB} = \frac{1}{3} \overline{u} \lambda_{A,B}
$$
- $\overline{u}$: average molecular velocity
- $\lambda$: mean free path between collisions
:::
:::{.column width="50%"}
Assumptions:
- Rigid sphere type molecules (what are they?)
- No interaction upon collisions
- Collisions are elastic (momentum conserved)
- Good for dilute gases (low $P$)
- Not accurate otherwise
:::
:::
---
## Molecular Diffusivity -- Chapman-Enskog Theory
We can take real interaction between molecules into the kinetic theory!
```{=tex}
\begin{align}
D_{AB} &= \frac{1.8583\times{}10^{-7} T^{3/2}}
{p_T \sigma_{AB}^2 \Omega_{D, AB}} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\
&\propto \frac{T^{\frac{3}{2}}}{p_T} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}}
\end{align}
```
- $m_A$, $m_B$, molecular weight
- $\sigma_{AB}$: average collision radius between A and B
- $\Omega_{D, AB}$: Lennard-Jones collision integral
- $\Omega_{D, AB}=1$ for elastic collision
- Chapman-Enskog theory accounts for non-elastic collision using $\Omega_{D, AB}\neq1$
---
## Chapman-Enskog Theory: How to Use
```{=tex}
\begin{align}
D_{AB} = \frac{1.8583\times{}10^{-7} T^{3/2}}
{p_T \sigma_{AB}^2 \Omega_{D, AB}} \left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}}
\end{align}
```
The Chapman-Enskog theory formula in *Geankoplis book* need to use the following units:
- $T$: absolute temperature in $\text{K}$
- $m_A$, $m_B$: molecular weight in $\text{kg} \cdot (\text{kg mol})^{-1}$ or $\text{g} \cdot (\text{g mol})^{-1}$
- $p_T$: absolute pressure in $\text{atm}$
- $\sigma_{AB}$: average collision diameter in Å
- $\Omega_{D, AB}$: collision integral (dimensionless)
Resulting $D_{AB}$ is in $\text{m}^2 \cdot \text{s}^{-1}$
---
## Chapman-Enskog Theory & Lennard Jones Potential
- Parameters $\sigma_{AB}$ and $\Omega_{D, AB}$ can be derived using Lennard-Jones (LJ) potential
- LJ potential described the interaction energy $U_{AB}$ between 2 molecules at distance $r$ follows:
```{=tex}
\begin{align}
U_{AB}(r) = 4\epsilon_{AB}\left[
(\frac{\sigma_{AB}}{r})^{12} - (\frac{\sigma_{AB}}{r})^{6}
\right]
\end{align}
```
How to get the parameters from table:
- $\sigma_{AB} = (\sigma_{A} + \sigma_{B})/2$
- $\epsilon_{AB} = \sqrt{\epsilon_A \epsilon_B}$
- $\Omega_{D, AB}$: get interpolated table values as function of $T^*=k_B T / \epsilon_{AB}$
::: {.callout-note}
Check online [course materials]() for the $\Omega_{D, AB}$ table!
:::
---
## Molecular Diffusivity Theory -- Fuller Method
The Chapman Enskog theory can be difficult to use, engineers need some simplied empirical rules.
```{=tex}
\begin{align}
D_{AB} &= \frac{1.0\times{}10^{-7} T^{1.75} }{p_T \left[ (\sum \nu_A)^{1/3} + (\sum \nu_B)^{1/3}\right]^2}
\left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}} \\
&\propto \frac{T^{1.75}}{p_T}
\end{align}
```
- Mainly to overcome the complicated estimation of $\Sigma_{D, AB}$ in Chapman-Enskog Theory
- $\sum \nu_i$ sum of structural volume increments
- $\sum \nu_i$ can be estimated from individual atoms
- Easier to use than the Chapman-Enskog Theory, but less accurate
---
## Fuller Method: How to Use
```{=tex}
\begin{align}
D_{AB} = \frac{1.0\times{}10^{-7} T^{1.75} }{p_T \left[ (\sum \nu_A)^{1/3} + (\sum \nu_B)^{1/3}\right]^2}
\left(\frac{1}{m_A} + \frac{1}{m_B} \right)^{\frac{1}{2}}
\end{align}
```
The Fuller method formula in *Geankoplis book* need to use the following units:
- $T$: absolute temperature in $\text{K}$
- $m_A$, $m_B$: molecular weight in $\text{kg} \cdot (\text{kg mol})^{-1}$ or $\text{g} \cdot (\text{g mol})^{-1}$
- $p_T$: absolute pressure in $\text{atm}$
- $\nu_{A}$, $\nu_{B}$: structural volume increments (dimensionless)
Resulting $D_{AB}$ is in $\text{m}^2 \cdot \text{s}^{-1}$
## How to Use the Fuller Method From a Table
We need to determine $\sum \nu_A$ and $\sum \nu_B$,
*Check Table 6.2-2 of Geankoplis 4th ed*.
- $\sum \nu_i$ are **dimensionless** numbers
- For known gases in the table, use its value in the table
- Air: $\nu = 20.1$
- O$_2$: $\nu = 16.6$
- For an unknown gas, use its chemical composition
- For chemical formula $\text{C}_x \text{H}_y \text{O}_z$,
$$
\sum \nu(\text{C}_x \text{H}_y \text{O}_z)
= \nu(\text{C}) \cdot x + \nu(\text{H}) \cdot y + \nu(\text{O}) \cdot z
$$
## Estimating $D_{AB}$ At Different $(T, P)$
For the same pair of (A, B), both the Chapman-Enskog and Fuller methods have the same form
$$
D_{AB} \propto \frac{T^n}{P}
$$
This means we can find one existing $D_{AB}$ value from table and extrapolate:
$$
\frac{D_{AB}\vert_1}{D_{AB}\vert_2}
= \left(\frac{T_1}{T_2}\right)^{n}
\left(
\frac{P_2}{P_1}
\right)
$$
Fuller method is often used in chemical engineering, where $n=1.75$.
---
## Example 1: Chapman-Enskog Theory vs Fuller Method
Question: calculate the diffusivity $D_{AB}$ for methan--ethan system at 313 K and 1 atm.
::: {.columns}
::: {.column width="50%"}
#### Chapman-Enskog Theory
- $m_A=16.04$, $m_B=30.07$
- $\rho_A (Å)=3.822$, $\rho_B (Å)=4.418$
- $\epsilon_A = k_B * (137\ \text{K})$, $\epsilon_B = k_B * (230\ \text{K})$
- $\Omega_{D, AB} = 1.125$ in this case
:::
::: {.column width="50%"}
#### Fuller Method
- $m_A=16.04$, $m_B=30.07$
- $\nu(\text{C})=16.5$, $\nu(\text{H})=1.98$
:::
:::
The experimental value at this condition is $D_{AB}=1.84\times 10^{-5}\ \text{m}^2\cdot s^{-1}$. Compare the percent errors in both methods.
::: {.content-visible when-format="html" unless-format="revealjs"}
---
## Solution to Example 1:
```{python}
#| echo: false
import marimo as mo
def chapman(ma, mb, T, p, sig_a, sig_b, Omega):
coeff = 1.8583e-7
numerator = coeff * T ** 1.5
denominator = p * ((sig_a + sig_b) / 2) ** 2 * Omega
mass_inv = (1/ma + 1/mb) ** 0.5
return numerator / denominator * mass_inv
def fuller(ma, mb, T, p, nu_a, nu_b):
coeff = 1.0e-7
numerator = coeff * T ** 1.75
denominator = p * (nu_a ** (1/3) + nu_b ** (1/3)) ** 2
mass_inv = (1/ma + 1/mb) ** 0.5
return numerator / denominator * mass_inv
def nu_ch(x_c, x_h):
nu_c = 16.5
nu_h = 1.98
return nu_c * x_c + nu_h * x_h
def calculate():
ma = 16.04
mb = 30.07
symb_a = (1, 4)
symb_b = (2, 6)
_T = 313
_p = 1.0
sig_a = 3.822
sig_b = 4.418
Omega = 1.125
v_chap = chapman(ma, mb, _T, _p, sig_a, sig_b, Omega)
v_fuller = fuller(ma, mb, _T, _p, nu_ch(*symb_a), nu_ch(*symb_b))
v_real = 1.84e-5
output = mo.vstack([
mo.md(f"""**Chapman-Enskog Theory**:
- Diffusivity (m^2/s) = {v_chap:.3e}
- Percentage error: {abs((v_chap - v_real) / v_real) * 100:.2f}%
"""),
mo.md(f"""
**Fuller Method**:
- Diffusivity (m^2/s) = {v_fuller:.3e}
- Percentage error: {abs((v_fuller - v_real) / v_real) * 100:.2f}%
"""
)])
return output
calculate()
```
:::
---
## Summary
- Diffusivity $D_{AB}$ value is the key to solve the transport problem in gases
- $D_{AB}$ can be measured from experiments, but not exhaustively
- Several theories predict the value for $D_{AB}$ with certain accuracy
- Chapman-Enkog theory and Fuller method both have $D_{AB}\propto T^n/P$ form
- Fuller method more often used as it can approximate $D_{AB}$ solely by taking values from table