MATE 664 Lecture 01

Thermodynamics and Kinetics

Dr. Tian Tian

2026-01-05

Land Acknowledgement

The University of Alberta acknowledges that we are located on Treaty 6 territory, and respects the histories, languages, and cultures of the First Nations, Métis, Inuit, and all First Peoples of Canada, whose presence continues to enrich our vibrant community.

Learning Outcomes

After today’s lecture, you will be able to:

• Identify the key components of the course syllabus, content and grading schemes.
• Recall common interaction methods and resources available in the course.
• Recall basic concepts in thermodynamics and kinetics
• State assumptions of equilibrium
• Describe the influence of entropy in kinetic systems

Course Information

• Course: MAT E 664 – Kinetics of Materials
• Term: Winter 2026
• Lectures: Mon & Wed
• Time: 14:00 – 15:20
• Location: HC 2-14

Meet the Instructor

• Office: DICE 12-245

• Email: tian.tian@ualberta.ca

• Office hour: by appointment

• I joined CME in 2025 as assistant professor.

• Research fields: machine learning, multiscale materials simulations, computational tools

• Let’s enjoy learning together!

TAs & Seminar Sessions

• Teaching Assistant
  • Hanlin Wang — hanlin7@ualberta.ca
• Course & Assignment Questions
  • No formal seminar or lab sessions
  • Questions related to course content or assignments
  • Please book an appointment with the TA (and instructor) as needed
• Support Format
  • One-on-one or small-group discussions
  • Concept clarification and guidance

Course Grading

• Assignments: 25%
  • 4 assignments (best 3 counted)
  • Submission via Canvas
• Final Project: 30%
  • Research-related topic
  • In-class oral presentation
• Final Exam: 45%
  • In person, open book
  • Apr 20, 2026 · 1:00 p.m.

Details please see the course syllabus

Textbook and References

Our primary textbooks for this course are:

• Kinetics of Materials by R.W. Balluffi, S.M. Allen, and W.C. Carter.

• Materials Kinetics: Transport and Rate Phenomena by John C. Mauro.

What Will We Learn in MAT E 664 (1)?

Theory: irreversible thermodynamics & driving forces

\[ \text{Flux} = \text{Kinetic coefficients} \times \text{Driving Force} \]

What Will We Learn in MAT E 664 (2)?

Mass transport on solid material interfaces: \(v_{step} = \beta (c - c_{eq})\)

¹

1. Image credit: A.R. Verma

## What Will We Learn in MAT E 664 (3)?

Nucleation theory: \(r_{c} = -\dfrac{2\gamma}{\Delta G_v}\)

¹

1. Image credit: crystalverse.com

What Will We Learn in MAT E 664 (4)?

Spinodal Decomposition (Pattern Formation) \[ \dfrac{\partial c}{\partial t} = \nabla \cdot \left( M \nabla \left[ \dfrac{\partial f(c)}{\partial c} - \kappa \nabla^{2} c \right] \right) \]

¹

1. Image credit: Mathis Plapp, École Polytechnique (FR)

Interaction Time!

We will use Wooclap in this course for real-time interactions.

Participation link 👉 https://app.wooclap.com/664L01?from=instruction-slide

Results to be published after the class

Thermodynamics vs. Kinetics

Feature	Thermodynamics	Kinetics
Greek Name	Therme (heat) + dynamis (power)	Kinetikos (of motion)
Focus	Eventually: Predicts the final state	Rate: How fast a process occurs
General Form	Free energy change (\(\Delta G\))	Reaction rates, flux, activation energy
Condition	Equilibrium	Non-equilibrium

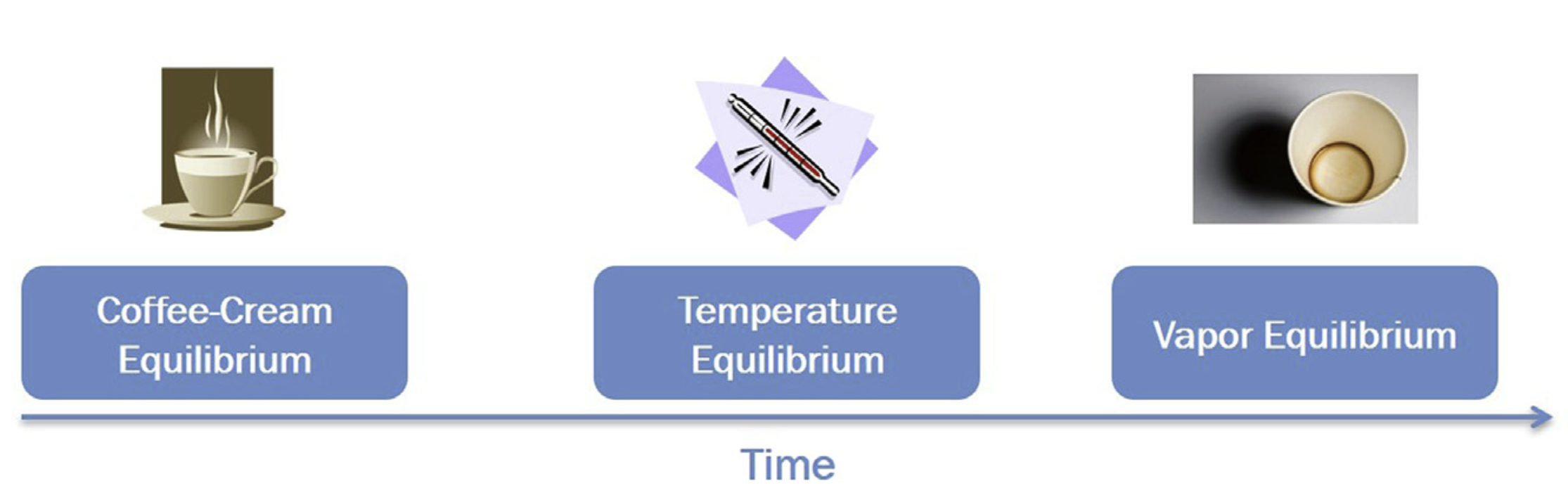
The True Meaning of Equilibrium

Equilibrium is a balance of time scales: \[ \tau_{\text{observation}} \gg \tau_{\text{process}} \]

• Thermodynamic descriptions are relevant when the observation time scale is much larger than the time scale of the processes reaching equilibrium.
• It’s about specific processes reaching a steady state, not necessarily the entire system.

¹

1. Image credit: John C. Mauro

Kinetic Processes

Kinetic processes are distinct from thermodynamic equilibrium:

1. Conditions: Occur away from equilibrium.
2. Cause Require a thermodynamic driving force.
3. Rate: Coupled with a rate parameter or coefficient.

Irreversible Thermodynamics is key to understanding these processes (Lecture 2).

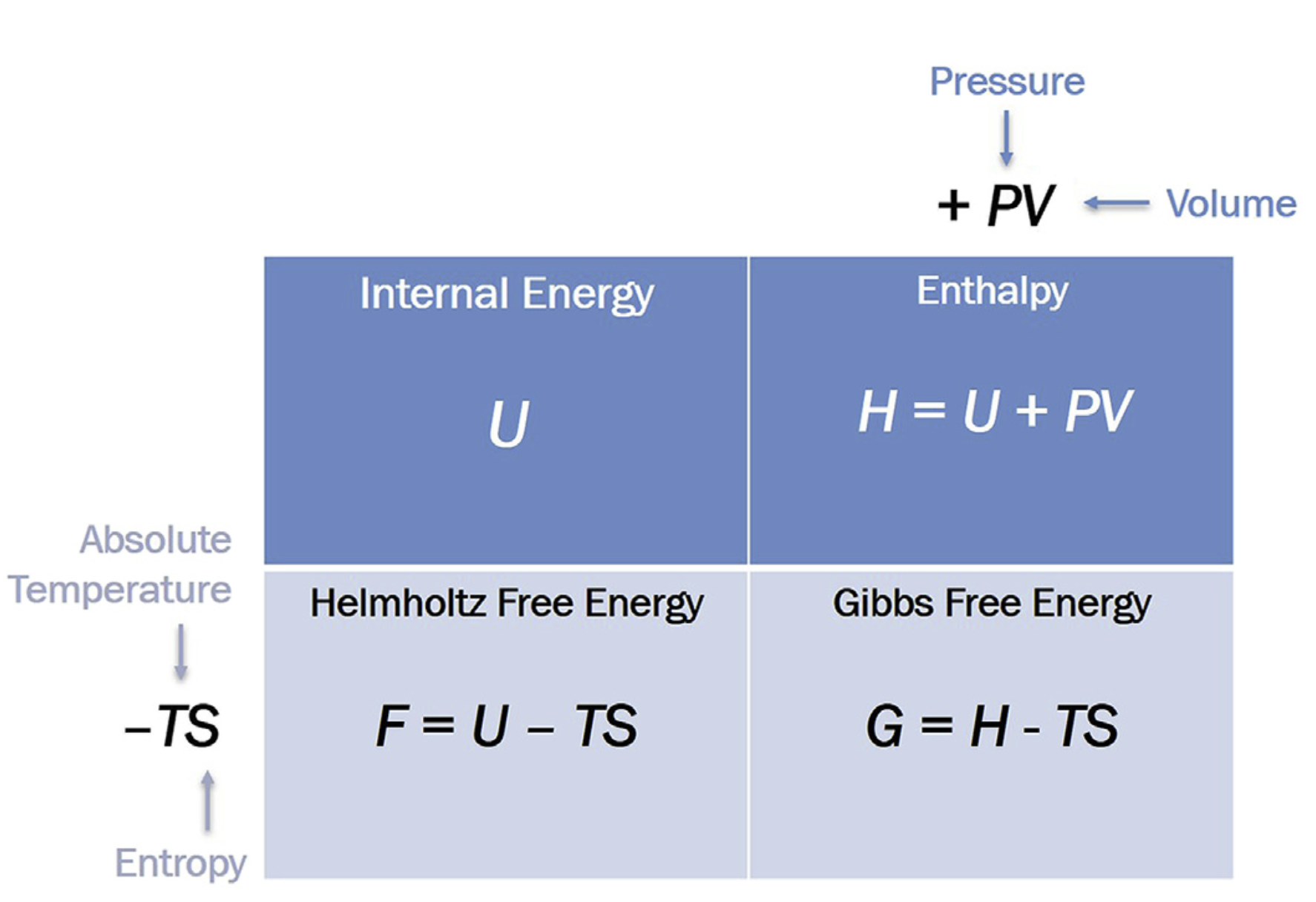
Classical Thermodynamics Revisited

¹

1. Image credit: John C. Mauro

## Thermodynamic Interplay Between \(H\) and \(S\)

Whether a process from A → B is spontaneous or non-spontaneous depends on the sign of free energy difference, \(\Delta G = G_{B} - G_{A}\).

¹

• What is \(\Delta G\) for a reversible process at equilibrium?: \(\Delta G = 0\),
• How can we check the stability of a certain material at \(P, T\)?: Use the phase diagram!

1. Image credit: John C. Mauro

How Stable Is Diamond?

• Which phase is the most stable at r.t. & 1 atm?
• Should we worry our diamond rings turn into pencil?

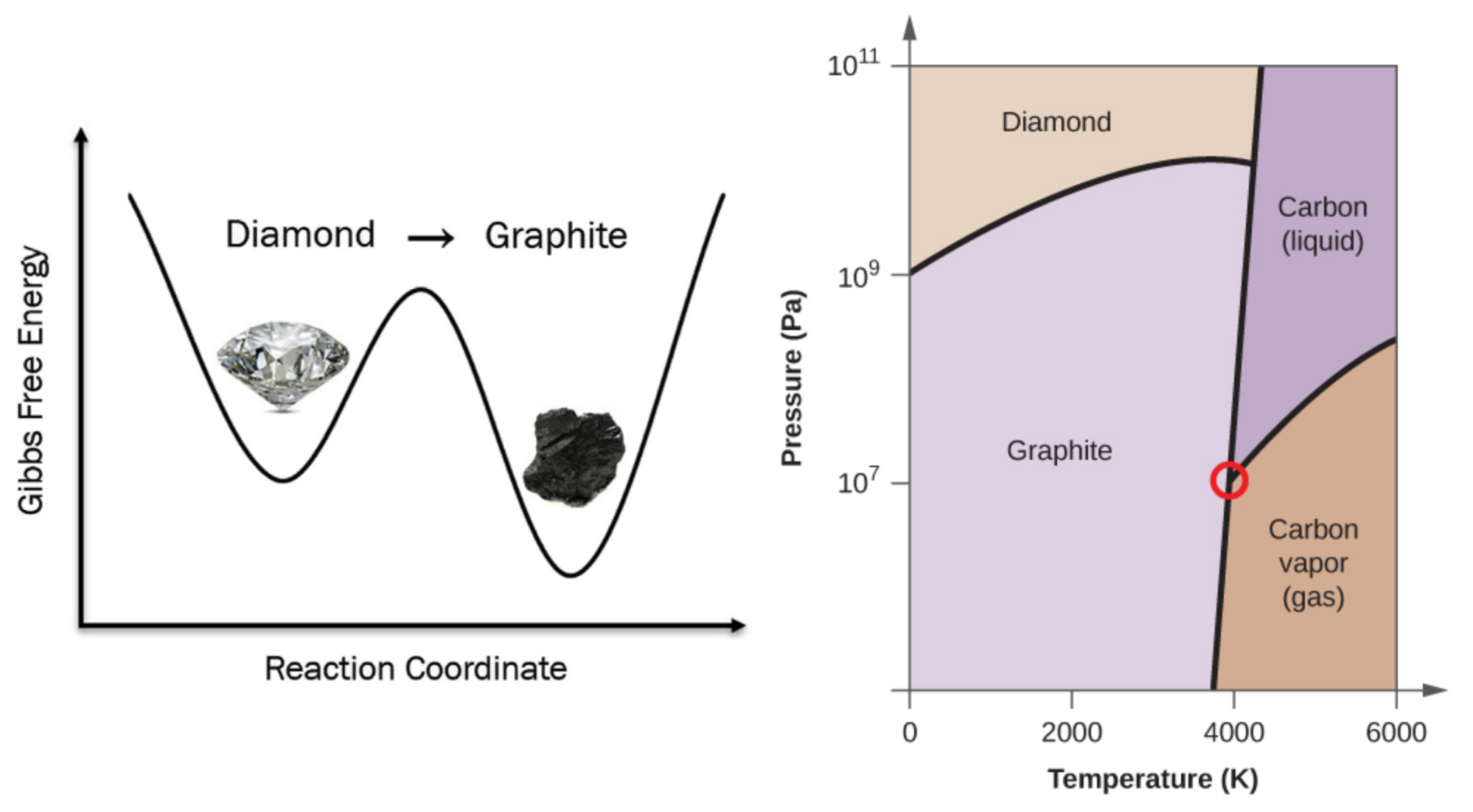
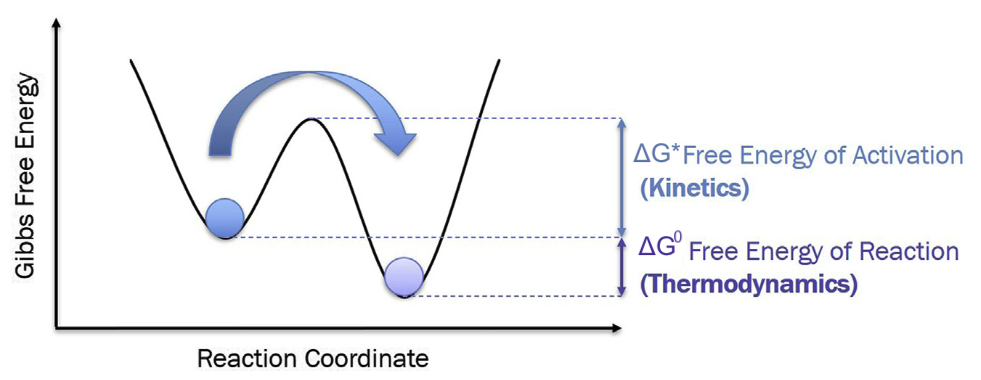
Two-State model of Thermodynamics vs Kinetics

• \(\Delta G^0\): Free energy of reaction → will reaction happen? (Thermodynamics)
• \(\Delta G^*\): Free energy of activation → how likely / fast? (Kinetics)

Arrhenius Plot Demo

Where Does Entropy \(S\) Come From?

• Claussius (1865) Classical thermodynamics.
  • Entropy is a state variable of internal energy.
  • \(dU(S, V) = TdS - pdV\)
• Boltzmann (1877) Statistical mechanics.
  • Entropy is a measure of accessible microstates (atoms + probability!)
  • \(S = k_B \log(\Omega)\)

Why The Logarithm?

• \(S\) as an extensive quantity → Additive \(S_T = S_1 + S_2\)
• \(\Omega\) as microstates is multiplicative → \(\Omega_T = \Omega_1 \cdot \Omega_2\)
• If \(S = f(\Omega)\), then \(S_T = f(\Omega_T) = f(\Omega_1 \cdot \Omega_2)\) → \(f(\Omega_1 \cdot \Omega_2) = f(\Omega_1) + f(\Omega_2)\)
• \(f(x) = C \log(x)\) is the unique solution using Cauchy’s functional equation results

Entropy IS NOT Disorder!

• Common statement of entropy is measure of disorder
• Boltzmann equation measures how many possibilities of arrangement
• Disorder is not uniquely linked to number of microstates!

Entropy IS NOT Disorder – II!

• High entropy alloys (HEAs): Example of high configurational entropy material
• Many HEAs have much more ordered lattice than binary alloys

¹

1. Small 2024, 20, 2311929

What Should We Really Think of Entropy

• Arrow of time: mixed cream and coffee cannot be demixed
  • Newtonian dynamics is time-reversible
  • We cannot rewind to low entropy state from Newtonian dynamics!
• Loss of information:
  • Shannon entropy: \(S_{info} = -k_B \sum_i p_i \log(p_i)\)
  • Shannon entropy can be measured on the exact state!
• Uncertainty:
  • Link to Heisenberg’s principle \(\Delta x \Delta p \leq \hbar/2\)
  • See Hirschman Am. J. Math., 1957 79, 152

Where Can We Go From Here?

• Irreversible thermodynamics

  Real processes occur away from equilibrium, where entropy is produced.

• Entropy generation as a driving force

  Gradients in temperature, concentration, and chemical potential drive fluxes by increasing total entropy.

• From equilibrium to dynamics

  Entropy provides the unifying language for diffusion, heat flow, chemical reactions, and transport phenomena.

Stay Tuned!

Brief Introduction to Course AI Helper

• A Socratic Gemini chatbot aiming to help course learning and key concepts
• Access the AI helper here: 👉 https://gemini.google.com/gem/1c118102b2d1

  

Summary

What we learned today:

• Syllabus / course contents of MATE 664
• Kinetic rate and equilibrium
• Concept of entropy revisited
• Laws of thermodynamics revisited

See you next time!