CHE 318 Lecture 01
Introduction and Diffusion Laws
- Slides 👉 Open presentation🗒️
- PDF version of course note 👉 Open in pdf
- Handwritten notes 👉 Open in pdf
Land Acknowledgement
The University of Alberta acknowledges that we are located on Treaty 6 territory, and respects the histories, languages, and cultures of the First Nations, Métis, Inuit, and all First Peoples of Canada, whose presence continues to enrich our vibrant community.
Learning Outcomes
After today’s lecture, you will be able to:
- Identify the key components of the course syllabus, content and grading schemes.
- Recall common interaction methods and resources available in the course.
- Define basic concepts in mass transfer, including concentration, mass fraction, and molar flux.
- State Fick’s First Law of Diffusion and identify its components and units
- Describe the general shape of solutions for stationary Fick’s Law.
Course Information
- Course: CH E 318 – Mass Transfer
- Term: Winter 2026
- Lectures: Mon, Wed, Fri
- Time: 10:00 – 10:50
- Location: MEC 3-1
Meet the Instructor
Office: DICE 12-245
Email: tian.tian@ualberta.ca
Office hour: by appointment (will send survey in Canvas)
- Updated: office hour will now be Wednesday 11:15 - 12:15 at DICE 12-245
I joined CME in 2025. CHE 318 is my first course at UofA
Research fields: machine learning, multiscale materials simulations, computational tools
Let’s enjoy learning together!
TAs & Seminar Sessions
- Teaching Assistants
- Ethan Lockwood — elockwoo@ualberta.ca
- Prince (Nkenna) Ezeano — ezeano@ualberta.ca
- Seminar (Lab) Session
- Time: Tuesday 15:30 – 17:20
- Location: MEC 4-3
- What seminars are for
- Problem-solving practice
- Worked examples and discussion
- Concept clarification and Q&A
Course Grading
- Assignments: 25%
- 8 total (best 7 counted)
- Deadlines to be posted on Canvas.
- Midterm Exam: 30%
- In class (50 min), closed book
- Time to be determined by end of Janurary 2026
- Final Exam: 45%
- In person
- Scheduled Apr 15, 2026 · 8:30 a.m.
Details please see the course syllabus
Textbook
Our primary textbook for this course is:
- Christie J. Geankoplis. Transport Processes and Separation Process Principles (Includes Unit Operations), 4th Edition

What do Mass Transfer Study (1)?
Scent diffuser: \[ J = -D \nabla C \]

What do Mass Transfer Study (2)?
Thin-membrane gas exchange: \[ N_{A} = D_{A} \dfrac{C_{A,1} - C_{A,2}}{\delta} \]
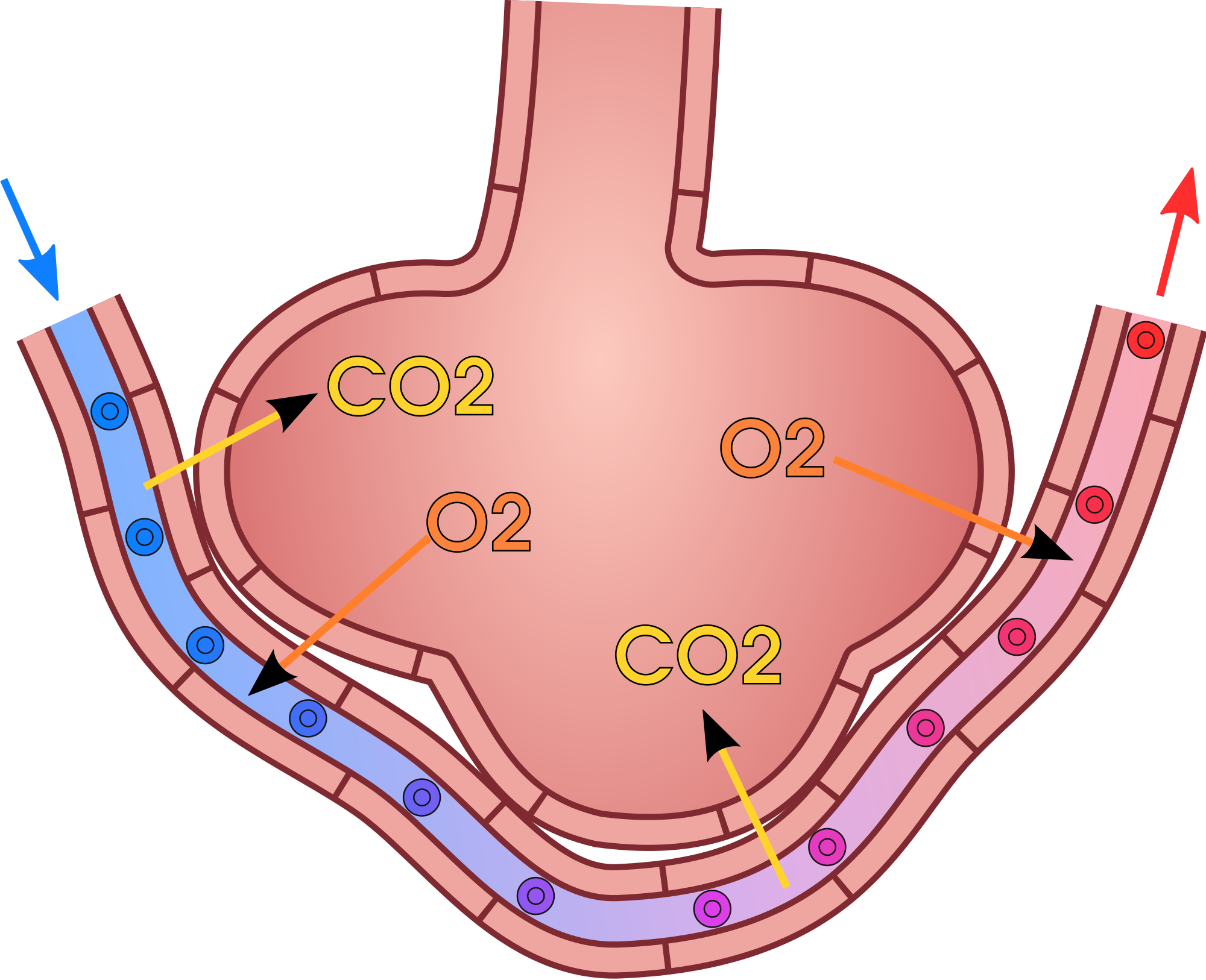
What do Mass Transfer Study (3)?
Packed tower:
\[ N_{A} = K_y (y_{AG} - y_{A}^*) \]
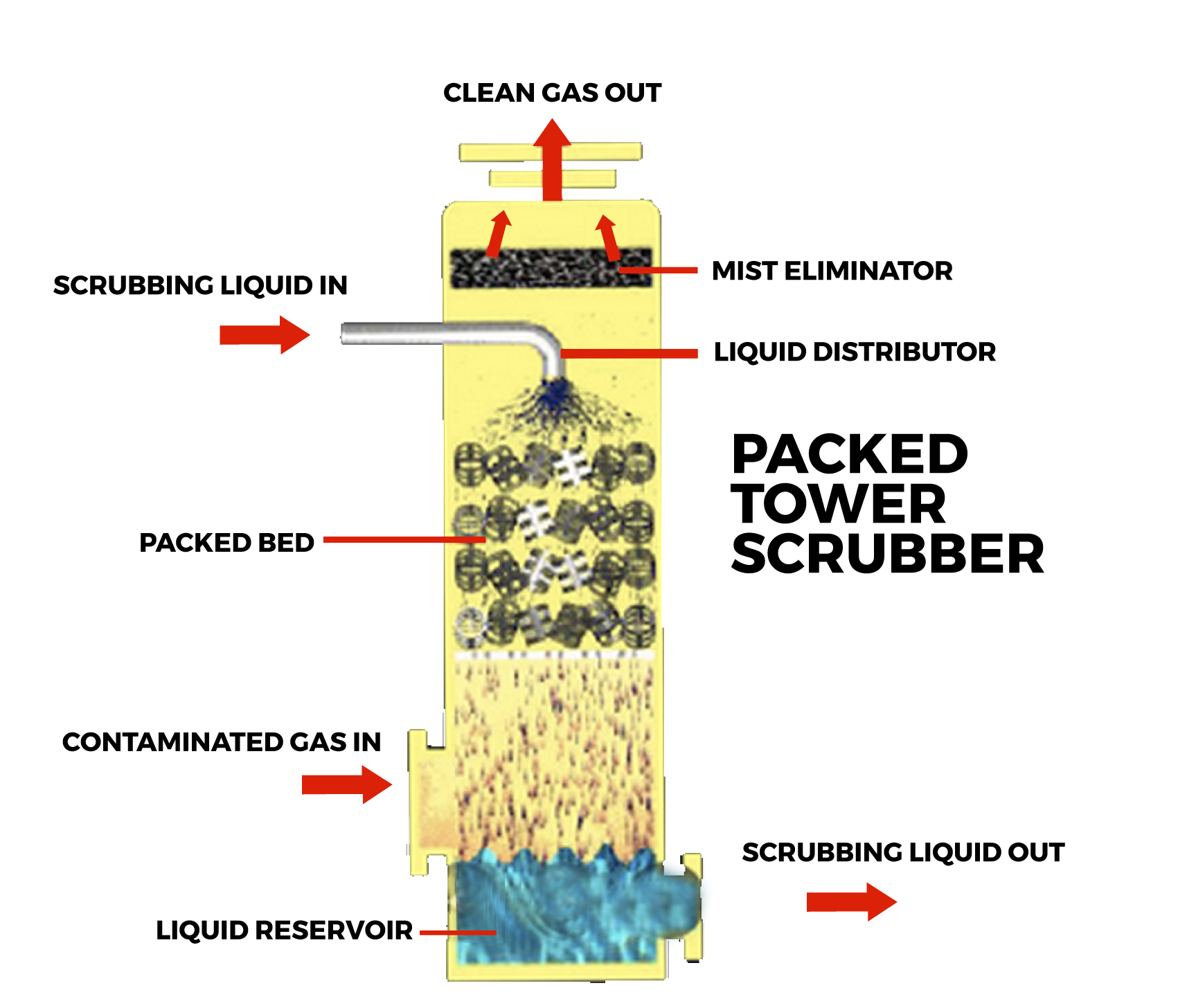
What do Mass Transfer Study (4)?
Manhattan project (\(U^{235}\) enrichment) ☢️:
\[ D \propto 1/\sqrt{M} \]

Let’s Get to Know You!
We will use Wooclap in this course!
Participation link: https://app.wooclap.com/318L01?from=instruction-slide
Results to be published after the class
Basic Quantities and Their Units in Mass Transfer (1)
We will only deal with SI units in this course!
(Molar) Concentraion of A: \(c_{A}\)
- Unit: \(\text{mol}\cdot\text{m}^{-3}\) or \(\text{kg mol}\cdot\text{m}^{-3}\)
- Total concentration: \(c_{T} = \sum_i c_{i} = c_A + c_B + \cdots\)
Molar fraction of A: \(x_{A} = \dfrac{c_A}{c_T}\)
Molar ratio (or binary mixture): \(Y_A = \dfrac{x_A}{x_B} = \dfrac{x_A}{1 - y_x}\)
- For ideal gas: \(x_A = \dfrac{p_A}{p_T}\) (partial pressure of A and total pressure, respectively)
Basic Quantities and Their Units in Mass Transfer (2)
Mass concentraion of A: \(\rho_A\) -Unit: \(\text{kg}\cdot\text{m}^{-3}\)
- Total mass concentration \(\rho_{T} = \sum_i \rho_{i} = \rho_A + \rho_B + \cdots\)
- \(c_i = \dfrac{\rho_i}{m_i}\) (\(m_i\): molecular weightunit \(\text{kg}\cdot\text{kg mol}^{-1}\) Non-SI!)
Mass fraction of A: \(w_A = \dfrac{\rho_A}{\rho_T}\), \(\sum_i w_i = 1\)
For chemists in this class, engineering unit \(\text{kg\ mol} = \text{kmol} = 1000\ \text{mol}\)
Introduction to Molecular Transport Equations (1)
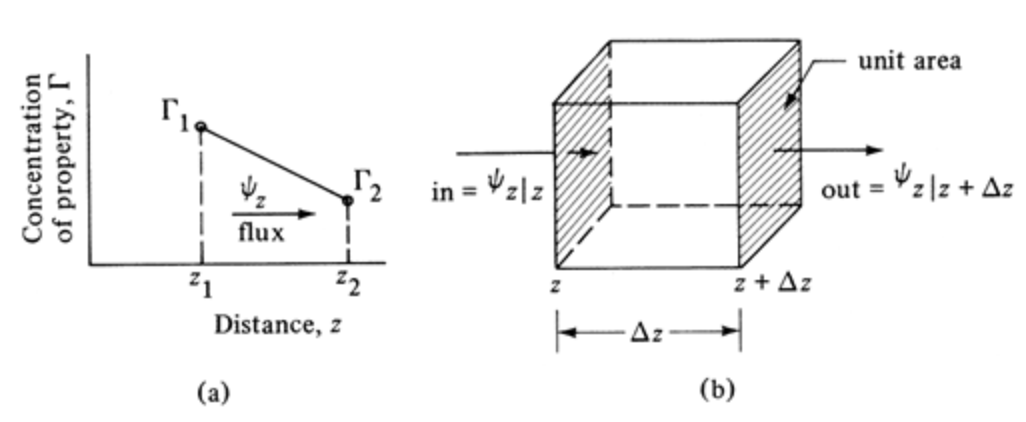
\[ \text{[rate of transfer process]} = \dfrac{\text{[driving force]}}{\text{[resistance]}} \]
Introduction to Molecular Transport Equations (2)
The governing equation for transport phenomena can also be written as
\[ \psi_z = -\delta \dfrac{d \Gamma}{dz} \]
Properties \(\Gamma\) to be transferred:
- Momentum (fluid mechanics)
- Heat (thermodynamics / heat transfer)
- Species (mass transfer)
Introduction to Molecular Transport Equations (3)
Units:
Flux (\(\psi_z\)): \(\text{[property]}\cdot{\text{m}^{-2}}\cdot{\text{s}^{-1}}\)
Concentration of property \(\Gamma\): \(\text{[property]}\cdot{\text{m}^{-3}}\)
What is the unit of coefficient \(\delta\)?: \(\text{m}^{2}\cdot{s^{-1}}\)
Why is there a negative sign before \(\delta\)?“: to match the sign of the flux
Fick’s First Law of Diffusion
The flux due to diffusion is described in Fick’s first law (more details next lecture).
Original form: \[ J^*_{Az} = - D_{AB} \dfrac{d c_A}{d z} \]
In molar fraction: \[ J^*_{Az} = - c_{T}D_{AB} \dfrac{d x_A}{d z} \]
For ideal gas (\(p_A = c_A RT\)) \[ J^*_{Az} = - D_{AB} \frac{1}{RT}\frac{d p_A}{d z} \]
Fick’s First Law in Velocity Term
The flux can also be written using velocity terms:
- Diffusive velocity: \[
J^*_{Az} = v_{Ad}\overline{c}_{A}
\]
- \(v_{Ad}\): diffusive velocity of A (\(\text{m}\cdot\text{s}^{-1}\))
- \(\overline{c}_{A}\): average concentration of A (\(\text{mol}\cdot\text{m}^{-3}\))
- Which reference frame is used?
Combining Diffusion and Convection
- Real-world mass transfer scenarios have diffusion + convection
- Using a lab frame, the total mass transfer flux can be written in diffusive + fluid velocities
The total molar flux of species A, \(N_A\), can be expressed as:
\[ N_A = J_{Az}^{*} + c_A v_m \]
- \(N_A\) is the total molar flux of A (\(\text{mol}\cdot\text{m}^{-2}\cdot\text{s}^{-1}\))
- \(J_{Az}^{*}\) is the diffusive molar flux of A relative to the molar average velocity (\(\text{mol}\cdot\text{m}^{-2}\cdot\text{s}^{-1}\))
- \(c_A\) is the molar concentration of A (\(\text{mol}\cdot\text{m}^{-3}\))
- \(v_m\) is the average velocity of the mixture (\(\text{m}\cdot\text{s}^{-1}\))
Governing Equation: Diffusion + Convection
For binary mixture of A and B, we have total flux for 2 components \(N\):
\[ N = N_A + N_B = v_m c_T = v_m (c_A + c_B) \]
Substituting \(v_m\) we get
\[ N_A = J_{Az}^* + \dfrac{c_A}{c_T}(N_A + N_B) \]
which further rewrites to
\[ N_A = -c_T D_{AB}\dfrac{d x_A}{dz} + \dfrac{c_A}{c_T}(N_A + N_B) \]
This is the governing equation for all steady-state mass transfer in the following lectures!
Brief Introduction to Course AI Helper
- A Socratic Gemini chatbot aiming to help course learning and key concepts
- Access the AI helper here: 👉 https://gemini.google.com/gem/f2d47200f0bf
Summary
What we learned today:
- Syllabus / course contents of CHE 318
- Basic concepts in mass transfer
- Fick’s 1st law of diffusion
- Governing equation of mass transfer
See you next time!
Footnotes
Geankoplis 4ed, eq 2.3-1↩︎