CHE 318 Lecture 14
Mass Transfer Coefficients (II)
- Slides 👉 Open presentation🗒️
- PDF version of course note 👉 Open in pdf
- Handwritten notes 👉 Open in pdf
Recap
- Introduction to mass transfer coefficients
- Link between mass transfer coefficient and diffusivity
- Introduction to boundary concentration problem
Learning Outcomes
After today’s lecture, you will be able to:
- Remember the flux equations using mass transfer coefficient in different phases
- Recall the motivation of using mass transfer coefficient
- Analyze mass transfer coefficients’ units
- Distinguish between mass transfer coefficients in different forms
Realistic Interfacial Concentration Profiles
At the boundary, it is often convenient to use the equilibrium concentration ratio between gas (\(c_i\)) and liquid (\(c_{Li}\)). This constant, often called the equilibrium distribution coefficient, is defined as:
\[\begin{align} K &= \frac{\text{[Conc. at gas side]}}{\text{[Conc. at liquid side]}} \\ &= \frac{c_{i}}{c_{Li}} \end{align}\]- Similarity: Henry’s law (\(H = \dfrac{p_{\text{gas}}}{c_{\text{aq}}}\)), remember in gas \(p_{\text{gas}} = c_{\text{gas}} RT\)
- We have already seen similar concepts in solubility in liquid / solid diffusion equations!
- \(K\) can be a value range from \(0\) to \(\infty\) 👉 what does that mean?
Interfacial Concentration Profile For Different \(K\)
- The interfacial concentration values depend on the value of \(K\)!
- What else determines the interfacial balance? 👉 matching of interfacial fluxes \(N_A\) at both sides!
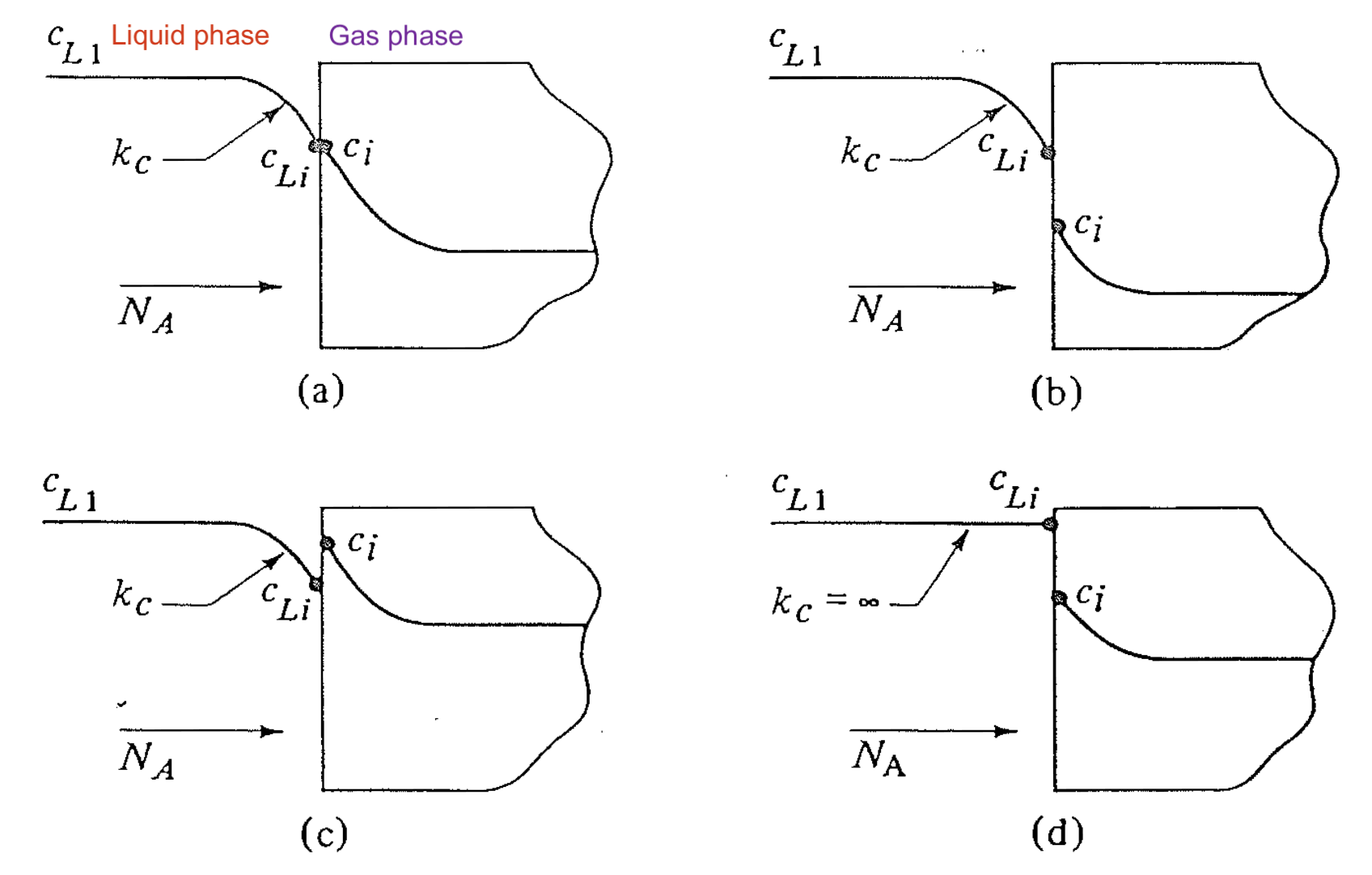
Match of Interfacial Fluxes
At equilibrium, if there is no resistance when transferring A between the interface, what is the mass balance equation?
\[\begin{align} \text{[In]}\vert_{\text{left}} - \text{[Out]}\vert_{\text{right}} + \text{[Gen]}\vert_{\text{interface}} &= \text{[Acc]}\vert_{\text{interface}} \\ N_A\vert_{\text{left}} = N_A\vert_{\text{right}} \end{align}\]How do we model \(N_A\) in each phase?
- May be a combination of diffusion and convection
- Fluid velocity at interface may be turbulent (hard to model)
- In general we use the phenomenal relation \(\text{[Flux]} = \text{[Driving Force]} / \text{[Resistance]}\)
General Flux Equation For Convective Transport Regime
- The driving force is the concentration difference “bulk concentration” and “interfacial concentration”
- The resistance is lumped into one coefficient \(k_c'\), mass transfer coefficient.
- \(k_c'\) is inversely related to the resistance.
- \(k_c'\) means driving force is concentration & convection term is EMCD-like
- The unit of \(k_c'\)? 👉 \(\text{m}\cdot\text{s}^{-1}\)
- \(k_c'\) can be \(\infty\)! 👉 No transfer resistance inside the bulk phase
Where Does \(k_c'\) Come From (I)?
Simplified view: transport resistance of A from bulk to the interface occurs inside an interfacial film with thickness \(\delta\). We can write \(N_A\) at steady state using already known results
- Case 1: EMCD / diffusion-controlled / dilute transport in liquid
- Case 2: transport in stagnant film with non-negligible convection
- Can be written both by \(k_c'\) or \(k_c\) terms
- One can expect \(k_c\) contain the \(1/x_{Bm}\) term!
Where Does \(k_c\) Come From (II)?
The mass transfer coefficient \(k_c\) is even valid for systems with effective \(D_{AB}\)!
- Case 3: mass transfer in porous solid materials
- Case 4: turbulent mass transfer
The turbulence in the fluid contributes to an additional term \(\epsilon_m\) in diffusion terms
\[\begin{align} N_A &= \boxed{\frac{D_{AB} + \epsilon_m}{\delta}} (c_{L, b} - c_{L, i}) \\ &= k_c' (c_{L, b} - c_{L, i}) \end{align}\]- \(\epsilon_m\) is the “Eddie diffusivity” (correction to \(D_{AB}\) due to turbulence)
- General case for \(\epsilon_m\) is non-trivial to solve!
Implications of Mass Transfer Coefficient \(k_c'\)
- Really convenient to use!
- In reality, \(k_c'\) is not a physics-based quantity, it depends on system / condition
- \(k_c' \propto D_{AB}^n\) in realistic systems
- We will discuss about different theories that explains the relation between \(k_c'\) and \(D_{AB}\) (penetration theory, film theory, boundary theory) in coming weeks
Balance Equations At Interfaces
We now have 2 equations to determine the interfacial concentrations!
- Equilibrium concentration distribution
- Flux matching
We can solve \(c_{L, i}\) and \(c_{g, i}\) given information about:
- Bulk concentrations \(c_{L, b}\), \(c_{g, b}\)
- Equilibrium distribution coefficient \(K\)
- Mass transfer coefficients \(k_c\) in each phase
Demonstration of Mixed Boundary Conditions
Mass Transfer Coefficient In Different Forms
When using \(k\) to express flux, we have the same form (Geankoplis Table 7.2.1)
- Flux equations for EMCD
- Flux equations for diffusion through stagnant B
But:
- \(k_c'\) and \(k_c\) are two different coefficients
- \(k_c'\), \(k_L'\), \(k_G'\) have different units
Naming Convention and Units
- Superscript: EMCD \(k'_{\text{driving force}}\); Convective / stagnant B \(k_{\text{driving force}}\)
| Phase / Driving force | Concentration \(c_A\) | Partial pressure \(p_A\) | Mole fraction (gas \(y_A\), liquid \(x_A\)) |
|---|---|---|---|
| Gas phase | \(k_c\), \(k_c'\) | \(k_G\), \(k_G'\) | \(k_y\), \(k_y'\) |
| Liquid phase | \(k_c\), \(k_c'\) | – | \(k_x\), \(k_x'\) |
| Liquid (alt. form) | \(k_L\), \(k_L'\) | – | – |
| Unit of \(k\) | \(\text{m}\cdot\text{s}^{-1}\) | \(\dfrac{\text{kg mol}}{\text{s} \cdot \text{m}^2 \cdot \text{Pa}}\) | \(\dfrac{\text{kg mol}}{\text{s} \cdot \text{m}^2 \cdot \text{mol frac}}\) |
Conversions Between Mass Transfer Coefficients
Gas phase
\[\begin{align} k_c' \, c_T &= k_c' \frac{p_T}{RT} = k_c \frac{p_{Bm}}{RT} \\ &= k_G' \, p_T = k_G \, p_{Bm} \\ &= k_y' = k_y \, y_{Bm} \\ &= k_c \, y_{Bm} \, c_T = k_G \, y_{Bm} \, p_T \end{align}\]- \(p\) : total pressure
- \(p_{Bm}\) : log-mean partial pressure of inert \(B\)
- \(y_{Bm}\) : log-mean mole fraction of \(B\)
- \(c_T = p_T/(RT)\)
Liquid phase
\[\begin{align} k_c' \, c &= k_L' \, c = k_L \, x_{Bm} \, c \\ &= k_L' \, \frac{\rho}{M} = k_x' = k_x \, x_{Bm} \end{align}\]- \(\rho\) : liquid density
- \(M\) : molecular weight
- \(x_{Bm}\) : log-mean mole fraction of solvent \(B\)
Summary
In this lecture, we talked about
- The difficulty of studying boundary problems in mass transfer
- The rise of equilibrium distribution coefficient \(K\) and mass transfer coefficient \(k\)
- Link between mass transfer coefficient \(k\) and transfer layer
What To Learn Next
The concept of mass transfer coefficient \(k\) is both beautiful and ugly.
- We gain the simplicity of expressing flux equations using simple formula,
- We lose physical understanding about its origin in many systems
In next lectures, we will see:
- How to use mass transfer coefficients for different phases (gas, liquid, solid)
- How convective fluid transport is expressed using coefficients
- How to perform mass transfer analysis based on transfer coefficients